
【题目】设函数![]() (
(![]() )
)
(Ⅰ)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)求![]() 单调区间;
单调区间;
(Ⅲ)若![]() 图象与
图象与![]() 轴关于
轴关于![]() ,
, ![]() 两点,求证:
两点,求证: ![]() .
.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C,所对的边分别为a,b,c.已知sinA+sinC=psinB(p∈R).且ac= ![]() b2 .
b2 .
(Ⅰ)当p= ![]() ,b=1时,求a,c的值;
,b=1时,求a,c的值;
(Ⅱ)若角B为锐角,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
: ![]() ,
, ![]() :
: ![]() (
(![]() ),从
),从![]() 上的点
上的点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,再从点
,再从点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() .设
.设![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: 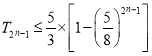 ;
;
(Ⅲ)若已知![]() (
(![]() ),记数列
),记数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为![]() 和
和![]() ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(Ⅰ)证明:CD⊥AE;
(Ⅱ)证明:PD⊥平面ABE;
(Ⅲ)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°.
(Ⅰ)证明:AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com