
【题目】在一次商贸交易会上,商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖.
(1)若抽奖规则是从一个装有![]() 个红球和
个红球和 ![]() 个白球的袋中一次取出
个白球的袋中一次取出![]() 个球,当两个球同色时则中奖,求中奖概率;
个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在![]() 之间赶到,乙计划在
之间赶到,乙计划在![]() 之间赶到,求甲比乙提前到达的概率.
之间赶到,求甲比乙提前到达的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)由题为古典概型,可先算出8个球取出2个的所有情况即(基本事件的个数),再算出取到2个为同色的基本事件数;代入古典概率概率公式可求;
(2)由题为时间问题,不可数。需化为几何概型来解决。因为有2人,可建立直角坐标系,化为面积比来算。
试题解析:(1)从袋中8个球中的摸出2个,试验的结果共有![]() (种)中奖的情况分为两种:
(种)中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为![]() ;
;
(ii)2个球都是白色,包含的基本事件数为![]() .
.
所以,中奖这个事件包含的基本事件数为25+9=34.因此,中奖概率为![]() . (2)设两人到达的时间分别为9点到10点之间的
. (2)设两人到达的时间分别为9点到10点之间的![]() 分钟、
分钟、![]() 分钟.
分钟.
用![]() 表示每次试验的结果,则所有可能结果为
表示每次试验的结果,则所有可能结果为![]() ;
;
记甲比乙提前到达为事件![]() ,则事件
,则事件![]() 的可能结果为
的可能结果为![]() .
.
如图所示,试验全部结果构成区域Ω为正方形![]() .
.
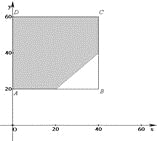
而事件![]() 所构成区域是正方形内的阴影部分.
所构成区域是正方形内的阴影部分.
根据几何概型公式,得到![]() .
.
所以,甲比乙提前到达的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|﹣2.
(Ⅰ)若a=1,求不等式f(x)+|2x﹣3|>0的解集;
(Ⅱ)若关于x的不等式f(x)<|x﹣3|恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(
=( ![]() cosx,﹣
cosx,﹣ ![]() ),函数f(x)=(
),函数f(x)=( ![]() )
) ![]() ﹣2.
﹣2.
(Ⅰ)求函数f(x)的最小正周期T;
(Ⅱ)已知a,b,c分别为△ABC内角A,B,C的对边,其中A为锐角,a=2 ![]() ,c=4,且f(A)=1,求A,b和△ABC的面积S.
,c=4,且f(A)=1,求A,b和△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线过点P![]() 且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,
,
(1)系数为什么值时,方程表示通过原点的直线;
(2)系数满足什么关系时与坐标轴都相交;
(3)系数满足什么条件时只与x轴相交;
(4)系数满足什么条件时是x轴;
(5)设![]() 为直线
为直线![]() 上一点,证明:这条直线的方程可以写成
上一点,证明:这条直线的方程可以写成![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+sinx+cosx,以下说法中不正确的是( )
A.f(x)周期为2π
B.f(x)最小值为﹣ ![]()
C.f(x)在区间[0, ![]() ]单调递增
]单调递增
D.f(x)关于点x= ![]() 对称
对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com