
| A. | 10 | B. | $4\sqrt{10}$ | C. | 17 | D. | $2\sqrt{17}$ |
分析 求出共轭双曲线方程,判断A的位置关系,求出m,画出图形,判断PQ的位置,求解即可.
解答 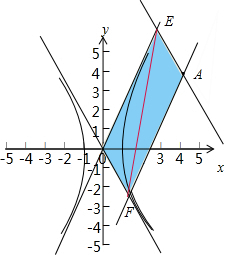 解:双曲线$\frac{y^2}{4}-{x^2}=1$的共轭双曲线为C为x2-$\frac{{y}^{2}}{4}$=1,画出双曲线图形,可知A在双曲线内部,与双曲线只有一点公共点,则m=2,
解:双曲线$\frac{y^2}{4}-{x^2}=1$的共轭双曲线为C为x2-$\frac{{y}^{2}}{4}$=1,画出双曲线图形,可知A在双曲线内部,与双曲线只有一点公共点,则m=2,
区域G如图:显然当PQ分别与区域的EF重合时,则$|{\overrightarrow{PQ}}|$取得最大值.双曲线的渐近线方程为:y=±2x,则EA的方程为:y-4=-2(x-4),AF的方程为:y-4=2(x-4).
由$\left\{\begin{array}{l}{y=2x}\\{2x+y-12=0}\end{array}\right.$可得E(3,6).
由$\left\{\begin{array}{l}{y=-2x}\\{2x-y-4=0}\end{array}\right.$可得F(1,-2).
则$|{\overrightarrow{PQ}}|$的最大值为:$\sqrt{(3-1)^{2}+(6+2)^{2}}$=2$\sqrt{17}$.
故选:D.
点评 本题考查双曲线的简单性质的应用,涉及线性规划,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆A:(x+1)2+y2=16,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
如图,圆A:(x+1)2+y2=16,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x≥0,x2+x-1<0”的否定是“?x<0,x2+x-1<0” | |
| C. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0,或x>2} | B. | {x|0<x<2} | C. | {x|0≤x<1} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
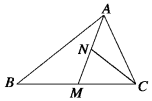
| A. | △ABM∽△ACB | B. | △ANC∽△AMB | C. | △ANC∽△ACM | D. | △CMN∽△BCA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com