
| 5 |
| 3 |
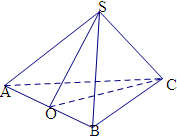 解:由于SA=SB=2,且SA⊥SB,BC=
解:由于SA=SB=2,且SA⊥SB,BC=| 5 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
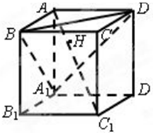 如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,有以下四个命题:
如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,有以下四个命题:
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
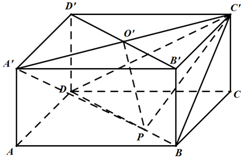 如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).
如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).
| ||
| 55 |
3
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| π |
| 4 |
| 1 |
| |PA| |
| 1 |
| |PB| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 图形符号 | 名 称 | 意 义 |
 | 表示一个算法的开始或者结束 | |
 | 表示算法中数据的输入或者结果的输出 | |
 | 赋值,执行计算语句,传送结果 | |
 | 根据给定的条件判断.当条件成立时,程序沿“是”方向执行,否则沿“否”方向执行 | |
 | 流程进行的方向 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 10 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| n |
| n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com