
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 ![]() =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心( ![]() ,
, ![]() )
)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() 的底面是正三角形,侧面
的底面是正三角形,侧面![]() 为菱形,且
为菱形,且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
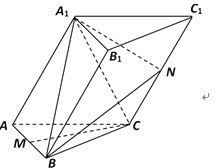
(I)求证:![]() ∥平面
∥平面![]() ;
;
(II)求证:![]() ;
;
(III)求BA1与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,一个焦点F(﹣2,0),且长轴长与短轴长的比是 ![]() .
.
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当 ![]() 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】E为正四面体D﹣ABC棱AD的中点,平面α过点A,且α∥平面ECB,α∩平面ABC=m,α∩平面ACD=n,则m、n所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1= ![]() ,an+1=
,an+1= ![]() (n∈N*).
(n∈N*).
(Ⅰ)求证:数列{ ![]() }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(Ⅱ)设bn+an=l(n∈N*),Sn=b1b2+b2b3+…+bnbn+1 , 试比较an与8Sn的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.求:
(1)“抽取的卡片上的数字满足a+b=c”的概率;
(2)“抽取的卡片上的数字a,b,c不完全相同”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com