
分析 先设出幂函数的解析式,然后根据题意求出解析式,根据导数的几何意义求出函数f(x)在x=$\frac{1}{2}$处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成一般式即可.
解答 解:f(x)是幂函数,设f(x)=xα
∵幂函数的图象经过点A($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),
∴$\frac{\sqrt{2}}{2}$=($\frac{1}{2}$)α
∴α=$\frac{1}{2}$
∴f(x)=${x}^{\frac{1}{2}}$
f′(x)=$\frac{1}{2\sqrt{x}}$
它在A点处的切线方程的斜率为f′($\frac{1}{2}$)=$\frac{\sqrt{2}}{2}$,
又过点A($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),
∴在A点处的切线方程为2$\sqrt{2}$x-4y+$\sqrt{2}$=0
故答案为:2$\sqrt{2}$x-4y+$\sqrt{2}$=0.
点评 本小题主要考查幂函数的定义和导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | $\frac{31}{16}$ | C. | $\frac{31}{32}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
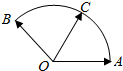 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧AB上变动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则$x+\frac{5}{2}y$的最大值是$\sqrt{13}$.
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧AB上变动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则$x+\frac{5}{2}y$的最大值是$\sqrt{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
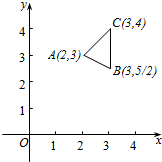 已知点(x,y)在△ABC所包围的阴影区域内(包含边界),若B是使得z=ax-y取得最大值的最优解,则实数a的取值范围为[-$\frac{1}{2}$,+∞).
已知点(x,y)在△ABC所包围的阴影区域内(包含边界),若B是使得z=ax-y取得最大值的最优解,则实数a的取值范围为[-$\frac{1}{2}$,+∞).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com