解:(1)∵函数f(x)=|x-a|为偶函数,
∴对任意的实数x,f(-x)=f(x)成立
即|-x-a|=|x-a|,
∴x+a=x-a恒成立,或x+a=a-x恒成立
∵x+a=a-x不能恒成立
∴x+a=x-a恒成立,得a=0.…(4分)
(2)当a>0时,|x-a|-ax=0有两解,
等价于方程(x-a)
2-a
2x
2=0在(0,+∞)上有两解,
即(a
2-1)x
2+2ax-a
2=0在(0,+∞)上有两解,…(6分)
令h(x)=(a
2-1)x
2+2ax-a
2,
因为h(0)=-a
2<0,所以
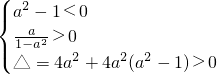
,故0<a<1;…(8分)
同理,当a<0时,得到-1<a<0;
当a=0时,f(x)=|x|=0=g(x),显然不合题意,舍去.
综上可知实数a的取值范围是(-1,0)∪(0,1).…(10分)
(3)令F(x)=f(x)•g(x)
①当0<a≤1时,则F(x)=a(x
2-ax),
对称轴

,函数在[1,2]上是增函数,
所以此时函数y=F(x)的最大值为4a-2a
2.
②当1<a≤2时,
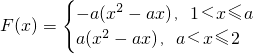
,对称轴
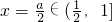
,
所以函数y=F(x)在(1,a]上是减函数,在[a,2]上是增函数,F(1)=a
2-a,F(2)=4a-2a
2,
1)若F(1)<F(2),即
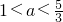
,此时函数y=F(x)的最大值为4a-2a
2;
2)若F(1)≥F(2),即
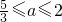
,此时函数y=F(x)的最大值为a
2-a.
③当2<a≤4时,F(x)=-a(x
2-ax)对称轴

,
此时
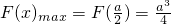
,
④当a>4时,对称轴
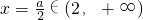
,此时
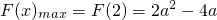
.
综上可知,函数y=F(x)在区间[1,2]上的最大值
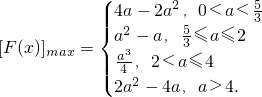
…(16分)
分析:(1)根据函数为偶函数,f(-x)=f(x)对任意实数x恒成立,即|-x-a|=|x-a|任意实数x成立,去绝对值然后比较系数,可得a=0;
(2)分三种情况加以讨论:当a>0时,将方程f(x)=g(x)两边平方,得方程(x-a)
2-a
2x
2=0在(0,+∞)上有两解,构造新函数h(x)=(a
2-1)x
2+2ax-a
2,通过讨论h(x)图象的对称轴方程和顶点坐标,可得0<a<-1;当a<0时,用同样的方法得到-1<a<0;而当a=0时代入函数表达式,显然不合题意,舍去.最后综合实数a的取值范围;
(3)F(x)=f(x)•g(x)=ax|x-a|,根据实数a与区间[1,2]的位置关系,分4种情况加以讨论:
①当0<a≤1时,则F(x)=a(x
2-ax),根据函数的单调增的性质,可得y=F(x)的最大值为F(2)=4a-2a
2;
②当1<a≤2时,化成两个二次表达式的分段函数表达式,其对称轴为
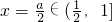
,得到所以函数y=F(x)在(1,a]上是减函数,在[a,2]上是增函数,最大值决定于F(1)与F(2)大小关系.因此再讨论:当
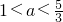
时,y=F(x)的最大值为F(2)=4a-2a
2;当
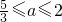
时,y=F(x)的最大值为F(1)=a
2-a;
③当2<a≤4时,F(x)=-a(x
2-ax),图象开口向下,对称轴

,恰好在对称轴处取得最大值:
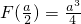
;
④当a>4时,F(x)=-a(x
2-ax),图象开口向下,对称轴
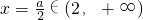
,在区间[1,2]上函数是增函数,故最大值为F(2)=2a
2-4a.
最后综止所述,可得函数y=F(x)在区间[1,2]上的最大值的结论.
点评:本题借助于含有字母参数的一次函数和含有绝对值的函数,通过讨论它们的奇偶性和单调性,以及讨论含有参数的方程根的个数,着重考查了函数的单调性的奇偶性、函数的零点和二次函数的图象与性质等知识点,属于难题.请同学们注意分类讨论和数形结合的数学思想在解决本题中所起的作用.

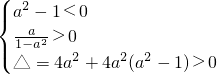 ,故0<a<1;…(8分)
,故0<a<1;…(8分) ,函数在[1,2]上是增函数,
,函数在[1,2]上是增函数,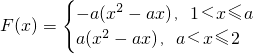 ,对称轴
,对称轴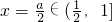 ,
,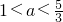 ,此时函数y=F(x)的最大值为4a-2a2;
,此时函数y=F(x)的最大值为4a-2a2;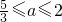 ,此时函数y=F(x)的最大值为a2-a.
,此时函数y=F(x)的最大值为a2-a. ,
,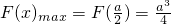 ,
,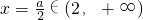 ,此时
,此时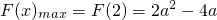 .
.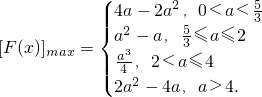 …(16分)
…(16分)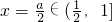 ,得到所以函数y=F(x)在(1,a]上是减函数,在[a,2]上是增函数,最大值决定于F(1)与F(2)大小关系.因此再讨论:当
,得到所以函数y=F(x)在(1,a]上是减函数,在[a,2]上是增函数,最大值决定于F(1)与F(2)大小关系.因此再讨论:当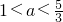 时,y=F(x)的最大值为F(2)=4a-2a2;当
时,y=F(x)的最大值为F(2)=4a-2a2;当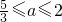 时,y=F(x)的最大值为F(1)=a2-a;
时,y=F(x)的最大值为F(1)=a2-a; ,恰好在对称轴处取得最大值:
,恰好在对称轴处取得最大值: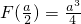 ;
;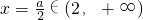 ,在区间[1,2]上函数是增函数,故最大值为F(2)=2a2-4a.
,在区间[1,2]上函数是增函数,故最大值为F(2)=2a2-4a.
