
【题目】在平面真角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为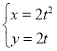 (t为参数),以原点O为极点,x轴正半轴为极轴,建立根坐标系.曲线
(t为参数),以原点O为极点,x轴正半轴为极轴,建立根坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 交于M,N两点,直线OM和ON的斜率分别为
交于M,N两点,直线OM和ON的斜率分别为![]() 和
和![]() ,求
,求![]() 的值.
的值.
 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点F与椭圆
的焦点F与椭圆![]() 的右焦点重合,过焦点F的直线l交抛物线于A,B两点.
的右焦点重合,过焦点F的直线l交抛物线于A,B两点.
(1)求抛物线C的方程;
(2)记抛物线C的准线与x轴的交点为H,试问:是否存在![]() ,使得
,使得![]() ,且
,且![]() 成立?若存在,求实数
成立?若存在,求实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.

(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商在销售200万台某型号手机时开展“手机碎屏险”活动、活动规则如下:用户购买该型号手机时可选购“手机碎屏险”,保费为![]() 元,若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这
元,若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这![]() 万台该型号手机全部销售完毕一年后,在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取
万台该型号手机全部销售完毕一年后,在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取![]() 名,每名用户赠送
名,每名用户赠送![]() 元的红包,为了合理确定保费
元的红包,为了合理确定保费![]() 的值,该手机厂商进行了问卷调查,统计后得到下表(其中
的值,该手机厂商进行了问卷调查,统计后得到下表(其中![]() 表示保费为
表示保费为![]() 元时愿意购买该“手机碎屏险”的用户比例);
元时愿意购买该“手机碎屏险”的用户比例);
(1)根据上面的数据求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)通过大数据分析,在使用该型号手机的用户中,购机后一年内发生碎屏的比例为![]() .已知更换一次该型号手机屏幕的费用为
.已知更换一次该型号手机屏幕的费用为![]() 元,若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于
元,若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于![]() 万元,能否把保费
万元,能否把保费![]() 定为5元?
定为5元?
x | 10 | 20 | 30 | 40 | 50 |
y | 0.79 | 0.59 | 0.38 | 0.23 | 0.01 |
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为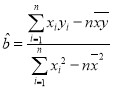 ,
,
![]() ,
,
参考数据:表中![]() 的5个值从左到右分别记为
的5个值从左到右分别记为![]() ,相应的
,相应的![]() 值分别记为
值分别记为![]() ,经计算有
,经计算有![]() ,其中
,其中![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com