
【题目】已知定义域为![]() 的奇函数
的奇函数![]() 的导函数为
的导函数为![]() ,当
,当![]() 时,
时,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 的大小关系正确的是( )
的大小关系正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据式子得出F(x)=xf(x)为R上的偶函数,利用f′(x)+![]() >0.
>0.
当x>0时,xf′(x)+f(x)>0,
当x<0时,xf′(x)+f(x)<0,判断单调性即可证明a,b,c 的大小.
定义域为R的奇函数y=f(x),
设F(x)=xf(x),
∴F(x)为R上的偶函数,
∴F′(x)=f(x)+xf′(x)
∵当x≠0时,f′(x)+![]() >0.
>0.
∴当x>0时,xf′(x)+f(x)>0,
当x<0时,xf′(x)+f(x)<0,
即F(x)在(0,+∞)单调递增,在(﹣∞,0)单调递减.
F(![]() )=a=
)=a=![]() f(
f(![]() )=F(ln
)=F(ln![]() ),F(﹣3)=b=﹣3f(﹣3)=F(3),F(ln
),F(﹣3)=b=﹣3f(﹣3)=F(3),F(ln![]() )=c=(ln
)=c=(ln![]() )f(ln
)f(ln![]() )=F(ln3),
)=F(ln3),
∵ln![]() <ln3<3,
<ln3<3,
∴F(ln![]() )<F(ln3)<F(3).
)<F(ln3)<F(3).
即a<c<b,
故选:C.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数,
是奇函数,![]() 为偶函数,
为偶函数,![]() 且(e是自然对数的底数).
且(e是自然对数的底数).
(1)分别求出![]() 和
和![]() 的解析式;
的解析式;
(2)记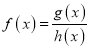 ,请判断
,请判断![]() 的奇偶性和单调性,并分别说明理由;
的奇偶性和单调性,并分别说明理由;
(3)若存在![]() ,使得不等式
,使得不等式![]() 能成立,求实数m的取值范围.
能成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解本市![]() 万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,发现其成绩服从正态分布
万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,发现其成绩服从正态分布![]() ,现从某校随机抽取了
,现从某校随机抽取了![]() 名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.
名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.

(1)估算该校![]() 名学生成绩的平均值
名学生成绩的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)求这![]() 名学生成绩在
名学生成绩在![]() 内的人数;
内的人数;
(3)现从该校![]() 名考生成绩在
名考生成绩在![]() 的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前
的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前![]() 名的人数记为
名的人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:若![]() ,则
,则![]() ,
, ![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·衢州调研)已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P在底面ABCD的射影,N是PC的中点.

(1)求证:平面MPB⊥平面PBC;
(2)若MP=MC,求直线BN与平面PMC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com