
【题目】如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:

(1)平面MENF⊥平面BDD′B′;
(2)当且仅当x=![]() 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
(3)四边形MENF周长L=f(x),x∈[0,1]是单调函数;
(4)四棱锥C′﹣MENF的体积V=h(x)为常函数,以上说法中正确的为( )
A. (2)(3) B. (1)(3)(4) C. (1)(2)(4) D. (1)(2)
【答案】C
【解析】
(1)利用面面垂直的判定定理去证明EF⊥平面BDD′B′;(2)四边形MENF的对角线EF是固定的,所以要使面积最小,则只需MN的长度最小即可;(3)判断周长的变化情况;(4)求出四棱锥的体积,进行判断.
(1)连结BD,B′D′,则由正方体的性质可知,EF⊥平面BDD′B′,所以平面MENF⊥平面BDD′B′,所以正确;
(2)连结MN,因为EF⊥平面BDD′B′,所以EF⊥MN,四边形MENF的对角线EF是固定的,所以要使面积最小,则只需MN的长度最小即可,此时当M为棱的中点时,即x![]() 时,此时MN长度最小,对应四边形MENF的面积最小.所以正确;
时,此时MN长度最小,对应四边形MENF的面积最小.所以正确;
(3)因为EF⊥MN,所以四边形MENF是菱形.当x∈[0,![]() ]时,EM的长度由大变小.当x∈[
]时,EM的长度由大变小.当x∈[![]() ,1]时,EM的长度由小变大.所以函数L=f(x)不单调.所以错误;
,1]时,EM的长度由小变大.所以函数L=f(x)不单调.所以错误;
(4)连结C′E,C′M,C′N,则四棱锥则分割为两个小三棱锥,它们以C′EF为底,以M,N分别为顶点的两个小棱锥.因为三角形C′EF的面积是个常数.M,N到平面C'EF的距离是个常数,所以四棱锥C'﹣MENF的体积V=h(x)为常函数,所以正确.
故选:C.


科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD
为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD![]() 平面PBC=
平面PBC=![]() .
.
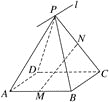
(1)求证:BC∥![]() ;
;
(2)MN与平面PAD是否平行?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , a1=a.当n≥2时,Sn2=3n2an+Sn﹣12 , an≠0,n∈N* .
(1)求a的值;
(2)设数列{cn}的前n项和为Tn , 且cn=3n﹣1+a5 , 求使不等式4Tn>Sn成立的最小正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为
与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为![]()

(1)求椭圆![]() 的离心率;
的离心率;
(2) 设点C、D、F2分别为椭圆![]() 的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆
的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆![]() 相交于M、N 两点,若
相交于M、N 两点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若向量 ![]() ,其中ω>0,记函数
,其中ω>0,记函数 ![]() ,若函数f(x)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次成公差为π的等差数列.
,若函数f(x)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次成公差为π的等差数列.
(1)求f(x)的表达式及m的值;
(2)将函数y=f(x)的图象向左平移 ![]() ,得到y=g(x)的图象,当
,得到y=g(x)的图象,当 ![]() 时,y=g(x)与y=cosα的交点横坐标成等比数列,求钝角α的值.
时,y=g(x)与y=cosα的交点横坐标成等比数列,求钝角α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数, ![]() 为常数.
为常数.
(1)确定![]() 的值;
的值;
(2)求证: ![]() 是
是![]() 上的增函数;
上的增函数;
(3)若对于区间![]() 上的每一个
上的每一个![]() 值,不等式
值,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() =bx+a,其中b=-20,a=
=bx+a,其中b=-20,a=![]() -b
-b![]()
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入—成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据市场调查,某型号的空气净化器有如下的统计规律,每生产该型号空气净化器![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(Ⅰ)求利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(Ⅱ)假定你是工厂老板,你该如何决定该产品生产的数量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,弦CD⊥AB于点M,点E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于点G. 
(1)求证:EF=EG;
(2)求线段MG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com