
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 四所高校中选2所.
四所高校中选2所.
(Ⅰ)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(Ⅱ)若已知甲同学特别喜欢![]() 高校,他必选
高校,他必选![]() 校,另在
校,另在![]() 三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
(ⅰ)求甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率;
高校的概率;
(ⅱ)记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 校的人数,求随机变量
校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(Ⅰ)![]() (Ⅱ)(ⅰ)
(Ⅱ)(ⅰ)![]() (ⅱ)分布列见解析,期望为
(ⅱ)分布列见解析,期望为![]() .
.
【解析】
(Ⅰ)先根据古典概型概率求甲同学选![]() 高校的概率,同理可得乙、丙同学选
高校的概率,同理可得乙、丙同学选![]() 高校的概率,最后根据独立事件概率乘法公式得结果,(Ⅱ)(ⅰ)先根据古典概型概率求甲同学选
高校的概率,最后根据独立事件概率乘法公式得结果,(Ⅱ)(ⅰ)先根据古典概型概率求甲同学选![]() 高校的概率以及乙、丙未选
高校的概率以及乙、丙未选![]() 高校的概率,最后根据独立事件概率乘法公式得结果,(ⅱ)先确定随机变量的取法,再分别求对应概率,列表得分布列,最后根据数学期望公式得结果.
高校的概率,最后根据独立事件概率乘法公式得结果,(ⅱ)先确定随机变量的取法,再分别求对应概率,列表得分布列,最后根据数学期望公式得结果.
(Ⅰ)甲从![]() 四所高校中选2所,共有AB,AC,AD,BC,BD,CD六种方法,
四所高校中选2所,共有AB,AC,AD,BC,BD,CD六种方法,
甲同学都选![]() 高校,共有AD,BD,CD三种方法,甲同学选
高校,共有AD,BD,CD三种方法,甲同学选![]() 高校的概率为
高校的概率为![]() ,
,
因此乙、丙同学选![]() 高校的概率皆为
高校的概率皆为![]() ,
,
因为每位同学彼此独立,所以甲、乙、丙三名同学都选![]() 高校的概率为
高校的概率为![]()
(Ⅱ)(ⅰ)甲同学必选![]() 校且选
校且选![]() 高校的概率为
高校的概率为![]() ,乙未选
,乙未选![]() 高校的概率为
高校的概率为![]() ,丙未选
,丙未选![]() 高校的概率为
高校的概率为![]() ,因为每位同学彼此独立,所以甲同学选
,因为每位同学彼此独立,所以甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率
高校的概率![]() ,
,
(ⅱ)![]()
因此![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
即分布列为
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
因此数学期望为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】当前,以“立德树人”为目标的课程改革正在有序推进。目前,国家教育主管部门正在研制的《新时代全面加强和改进学校体育美育工作意见》,以及将出台的加强劳动教育指导意见和劳动教育指导大纲,无疑将对体美劳教育提出刚性要求。为激发学生加强体育活动,保证学生健康成长,某校开展了校级排球比赛,现有甲乙两人进行比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满8局时停止。设甲在每局中获胜的概率为![]() ,且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养;若
的值评定学生的数学核心素养;若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食堂用餐的满意度进行评分.根据学生对食堂用餐满意度的评分,得到如图所示的率分布直方图,
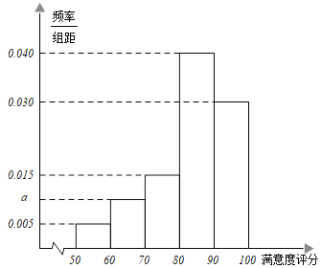
(1)求频率分布直方图中![]() 的值
的值
(2)规定:学生对食堂用餐满意度的评分不低于80分为“满意”,试估计该校在食堂用餐的3000名学生中“满意”的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为![]() .
.
(1)从袋中随机抽取两个球,求取出的球的编号之和为偶数的概率;
(2)先从袋中随机取一个球,该球的编号为![]() ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
①![]() 的单调递减区间;
的单调递减区间;
②当![]() 时,直线y=k与y=f (x)的图象有两个不同交点;
时,直线y=k与y=f (x)的图象有两个不同交点;
③函数y=f(x)的图象与![]() 的图象没有公共点;
的图象没有公共点;
④当![]() 时,函数
时,函数![]() 的最小值为2.
的最小值为2.
其中正确结论的序号是_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com