
【题目】设函数![]() ,
,![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,函数
时,函数![]() 恰有两个零点
恰有两个零点![]() ,证明:
,证明:![]()
【答案】(1) 当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)证明见解析.
【解析】分析:(1)对函数![]() 求导,令
求导,令![]() ,
,![]() ,分
,分![]() ,判断出单调性;(2)采用综合分析法证明, 由已知条件求出
,判断出单调性;(2)采用综合分析法证明, 由已知条件求出 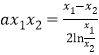 ,要证明
,要证明![]() ,即证
,即证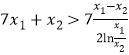 ,即证
,即证 ,令
,令![]() ,通过证明
,通过证明![]() ,得出结论。
,得出结论。
详解: (Ⅰ)![]() .
.
∵![]() ,∴由
,∴由![]() ,得
,得![]() ,即
,即![]() .
.
若![]() ,当
,当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
若![]() ,当
,当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| + | 0 | - |
| 单调递增 | 极大值 | 单调递减 |
综上,当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)∵当![]() 时,函数
时,函数![]() 恰有两个零点
恰有两个零点![]() ,
,![]()
![]() ,
,
则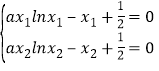 ,即
,即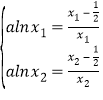 .
.
两式相减,得![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴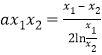 .
.
∴要证![]() ,即证
,即证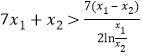 ,即证
,即证![]()
即证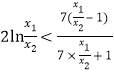
令![]()
![]() ,则即证
,则即证![]() .
.
设![]() ,即证
,即证![]() 在
在![]() 恒成立.
恒成立.
![]() .
.
∵![]() 在
在![]() 恒成立.∴
恒成立.∴![]() 在
在![]() 单调递增.
单调递增.
∵![]() 在
在![]() 是连续函数,
是连续函数,
∴当![]() 时,
时,![]()
∴当![]() 时,有
时,有![]() .
.


科目:高中数学 来源: 题型:
【题目】某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初始溶液含杂质2%,每过滤一次可使杂质含量减少![]() .
.
(1)写出杂质含量y与过滤次数n的函数关系式;
(2)过滤7次后的杂质含量是多少?过滤8次后的杂质含量是多少?至少应过滤几次才能使产品达到市场要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(3)为了激励同学们的学习热情,现评出一二三等奖,得分在![]() 内的为一等奖,得分在
内的为一等奖,得分在![]() 内的为二等奖, 得分在
内的为二等奖, 得分在![]() 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设![]() 为获得三等奖的人数,求
为获得三等奖的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为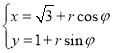 (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
,![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技公司研究开发了一种新产品,生产这种新产品的每天固定成木为30000元,每生产x件,需另投入成本为t元, 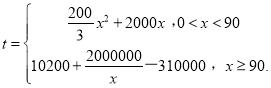 ,每件产品售价为10000元.(该新产品在市场上供不应求可全部卖完.)
,每件产品售价为10000元.(该新产品在市场上供不应求可全部卖完.)
(1)写出每天利润y关于每天产量x的函数解析式;
(2)当每天产量为多少件时,该公司在这一新产品的生产中每天所获利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com