
【题目】已知函数![]() ,实数
,实数![]() 且
且![]() .
.
(1)设![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)设![]() 且
且![]() 时,
时,![]() 的定义域和值域都是
的定义域和值域都是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的范围.
的范围.
【答案】(1)单调递增,证明见解析;(2)![]() ;(3)
;(3)![]() 且
且![]()
【解析】
(1)根据函数单调性定义作差判断函数单调性;
(2)根据单调性确定![]() ,
,![]() ,再转化为对应方程实根分布问题,根据韦达定理以及求根公式得
,再转化为对应方程实根分布问题,根据韦达定理以及求根公式得![]() 关于
关于![]() 的函数关系式,最后根据二次函数性质求最值得结果;
的函数关系式,最后根据二次函数性质求最值得结果;
(3)先根据绝对值定义化简不等式,变量分离转化为求对应函数最值,
(1)设![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
即![]() ,因此函数
,因此函数![]() 在
在![]() 上的单调递增.
上的单调递增.
(2)由(1)及![]() 的定义域和值域都是
的定义域和值域都是![]() 得
得![]() ,
,![]() ,
,
因此![]() ,
,![]() 是方程
是方程![]() 的两个不相等的正数根,
的两个不相等的正数根,
等价于方程![]() 有两个不等的正数根,
有两个不等的正数根,
即![]() 且
且![]() 且
且![]() ,
,
解得![]() ,
,
∴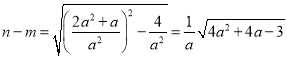
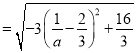 ,
,
∵![]() ,∴
,∴![]() 时,
时,![]() 最大值为
最大值为![]() .
.
(3)![]() ,则不等式
,则不等式![]() 对
对![]() 恒成立,
恒成立,
即![]() ,即不等式
,即不等式![]() 对
对![]() 恒成立,
恒成立,
令![]() ,易证
,易证![]() 在
在![]() 递增,同理
递增,同理![]() 在
在![]() 递减.
递减.
∴![]() ,
,![]() ,
,
∴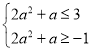 ,∴
,∴![]() 且
且![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知集合M是具有下列性质的函数![]() 的全体:存在实数对
的全体:存在实数对![]() ,使得
,使得![]() 对定义域内任意实数x都成立.
对定义域内任意实数x都成立.
(1)判断函数![]() ,
,![]() 是否属于集合
是否属于集合![]() ;
;
(2)若函数![]() 具有反函数
具有反函数![]() ,是否存在相同的实数对
,是否存在相同的实数对![]() ,使得
,使得![]() 与
与![]() 同时属于集合
同时属于集合![]()
![]() 若存在,求出相应的
若存在,求出相应的![]() ;若不存在,说明理由;
;若不存在,说明理由;
(3)若定义域为![]() 的函数
的函数![]() 属于集合
属于集合![]() ,且存在满足有序实数对
,且存在满足有序实数对![]() 和
和![]() ;当
;当![]() 时,
时,![]() 的值域为
的值域为![]() ,求当
,求当![]() 时函数
时函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 的内切圆与三边
的内切圆与三边![]() 的切点分别为
的切点分别为![]() ,已知
,已知![]() ,内切圆圆心
,内切圆圆心![]() ,设点A的轨迹为R.
,设点A的轨迹为R.
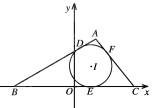
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使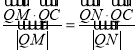 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对其定义域内的任意
对其定义域内的任意![]() ,
,![]() ,当
,当![]() 时总有
时总有![]() ,则称
,则称![]() 为紧密函数,例如函数
为紧密函数,例如函数![]() 是紧密函数,下列命题:
是紧密函数,下列命题:
![]() 紧密函数必是单调函数;
紧密函数必是单调函数;![]() 函数
函数![]() 在
在![]() 时是紧密函数;
时是紧密函数;
![]() 函数
函数![]() 是紧密函数;
是紧密函数;
![]() 若函数
若函数![]() 为定义域内的紧密函数,
为定义域内的紧密函数,![]() ,则
,则![]() ;
;
![]() 若函数
若函数![]() 是紧密函数且在定义域内存在导数,则其导函数
是紧密函数且在定义域内存在导数,则其导函数![]() 在定义域内的值一定不为零.
在定义域内的值一定不为零.
其中的真命题是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】裴波那契数列(Fibonacci sequence )又称黄金分割数列,因为数学家列昂纳多·裴波那契以兔子繁殖为例子引入,故又称为“兔子数列”,在数学上裴波那契数列被以下递推方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中a为常数,e是自然对数的底数,
,其中a为常数,e是自然对数的底数,![]() ,曲线
,曲线![]() 在其与y轴的交点处的切线记作
在其与y轴的交点处的切线记作![]() ,曲线
,曲线![]() 在其与x轴的交点处的切线记作
在其与x轴的交点处的切线记作![]() ,且
,且![]() .
.
(1)求![]() 之间的距离;
之间的距离;
(2)对于函数![]() 和
和![]() 的公共定义域中的任意实数
的公共定义域中的任意实数![]() ,称
,称![]() 的值为函数
的值为函数![]() 和
和![]() 在
在![]() 处的偏差.求证:函数
处的偏差.求证:函数![]() 和
和![]() 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在六棱锥P﹣ABCDEF中,六边形ABCDEF为正六边形,平面PAB⊥平面ABCDEF,AB=1,PA![]() ,PB=2.
,PB=2.
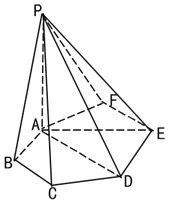
(1)求证:PA⊥平面ABCDEF;
(2)求直线PD与平面PAE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com