
【题目】设函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在以![]() 为首项,公比为
为首项,公比为![]() (
(![]() ,
,![]() )的数列
)的数列![]() ,
,![]() 使得数列
使得数列![]() 的每一项都是数列
的每一项都是数列![]() 的不同的项,若存在,求出所有满足条件的数列
的不同的项,若存在,求出所有满足条件的数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(参考公式: 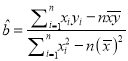 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在D上的函数f(x)满足:对任意x∈D,存在常数M>0,都有-M<f(x)<M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界。
(Ⅰ)判断函数f(x)=![]() -2x+2,x∈[0,2]是否是有界函数,请说明理由;
-2x+2,x∈[0,2]是否是有界函数,请说明理由;
(Ⅱ)若函数f(x)=1+![]() +
+![]() ,x∈[0,+∞)是以3为上界的有界函数,求实数a的取值范围。
,x∈[0,+∞)是以3为上界的有界函数,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和面内一点
,和面内一点![]() ,过点
,过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() ,试求
,试求![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校名教师参加我县“六城”同创“干部职工进网络,服务群众进社区”活动,他们的年龄均在25岁至50岁之间,按年龄分组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:

上表是年龄的频数分布表.
(1)求正整数![]() 的值;
的值;
(2)根据频率分布直方图估计我校这![]() 名教师年龄的中位数和平均数;
名教师年龄的中位数和平均数;
(3)从第一、二组用分层抽样的方法抽取4人,现在从这4人中任取两人接受咸丰电视台的采访,求从这4人中选取的两人年龄均在第二组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有一条光线从![]() 射出,并且经
射出,并且经![]() 轴上一点
轴上一点![]() 反射.
反射.
(1)求入射光线和反射光线所在的直线方程(分别记为![]() );
);
(2)设动直线![]() ,当点
,当点![]() 到
到![]() 的距离最大时,求
的距离最大时,求![]() 所围成的三角形的内切圆(即:圆心在三角形内,并且与三角形的三边相切的圆)的方程.
所围成的三角形的内切圆(即:圆心在三角形内,并且与三角形的三边相切的圆)的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() :
:![]() 相交所得的弦长为
相交所得的弦长为![]() .
.
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() ,
,![]() 是
是![]() 上异于原点
上异于原点![]() 的两个不同点,直线
的两个不同点,直线![]() 和
和![]() 的倾斜角分别为
的倾斜角分别为![]() 和
和![]() ,当
,当![]() ,
,![]() 变化且
变化且![]() 为定值
为定值![]() (
(![]() )时,证明:直线
)时,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过椭圆
,过椭圆![]() 右顶点和上顶点的直线
右顶点和上顶点的直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com