Question

在正方形ABCD-A₁B₁C₁D₁中，M、N、Q分别是棱D₁C₁、A₁D₁、BC的中点，点P在BD₁上且BP=

2

3

BD₁．则以下四个说法：
（1）MN∥平面APC；
（2）C₁Q∥平面APC；
（3）A、P、M三点共线；
（4）平面MNQ∥平面APC．
其中说法正确的是

 

．

Answer 1

考点：平面与平面平行的判定

专题：空间位置关系与距离

分析：观察正方体不难发现（1）因为直线在平面内；（4）平面与平面相交，是错误的；（2）在平面内找到直线和它平行（3）利用相似可以说明是正确的．

解答： 解：解：（1）MN∥AC，连接AM、CN，
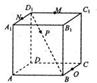
得AM、CN交与点P，即MN⊆面PAC，所以MN∥面APC是错误的；
（2）平面APC延展，可知M、N在平面APC上，AN∥C₁Q，
所以C₁Q∥面APC，是正确的；
（3）由BP=

2

3

BD₁，以及（2）△APB∽△D₁MP，
所以，A，P，M三点共线，是正确的；
（4）直线AP延长到M，则M在平面MNQ，
又在平面APC，面MNQ∥面APC，是错误的．
故答案为：（2）（3）．

点评：本题考查直线与平面平行，平面与平面平行的判定，三点共线问题，考查空间想象能力，是基础题．