
分析 根据题意,分2步进行分析:①、先在从5个奇数中任选3个奇数,安排在五位数的奇数位置,②、在剩余的6个数字中,任选2个,安排在五位数的偶数位置,求出每一步的选法数目,由分步计数原理计算可得答案.
解答 解:根据题意,1到9这9个数字中有5个奇数,4个偶数,
可以分2步进行分析:
①、先在从5个奇数中任选3个奇数,安排在五位数的奇数位置,有A53种选法;
②、在剩余的6个数字中,任选2个,安排在五位数的偶数位置,有A62种选法;
则奇数的位置上是奇数的排法有A53×A62=1800种;
故奇数的位置上是奇数的排法有1800种.
点评 本题考查排列、组合的应用,关键要根据题意,将问题转化,进行分类讨论.


科目:高中数学 来源: 题型:解答题
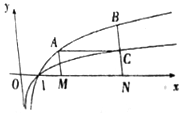 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,1) | B. | (2,+∞) | C. | $({-∞,-2})∪({\frac{1}{4},+∞})$ | D. | $({-∞,\frac{1}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{16}{13}$ | C. | $\frac{32}{13}$ | D. | $\frac{30}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
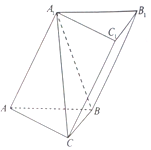 如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.
如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com