
【题目】已知三棱锥![]() 的所有顶点都在球
的所有顶点都在球![]() 的球面上,
的球面上,![]() 平面
平面![]() ,
,![]() ,
,![]() ,若球
,若球![]() 的表面积为
的表面积为![]() ,则三棱锥
,则三棱锥![]() 的侧面积的最大值为( )
的侧面积的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
由题意画出图形,设球O得半径为R,AB=x,AC=y,由球O的表面积为29π,可得x2+y2=25,写出侧面积,再由基本不等式求最值.
设球O得半径为R,AB=x,AC=y,
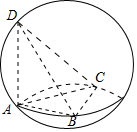
由4πR2=29π,得4R2=29.又x2+y2+22=(2R)2,得x2+y2=25.三棱锥A-BCD的侧面积:S=S△ABD+S△ACD+S△ABC=![]() 由x2+y2≥2xy,得xy≤
由x2+y2≥2xy,得xy≤![]() 当且仅当x=y=
当且仅当x=y=![]() 时取等号,由(x+y)2=x2+2xy+y2≤2(x2+y2),得x+y≤5
时取等号,由(x+y)2=x2+2xy+y2≤2(x2+y2),得x+y≤5![]() ,当且仅当x=y=
,当且仅当x=y=![]() 时取等号,∴S≤5
时取等号,∴S≤5![]() +
+![]() =
=![]() 当且仅当x=y=
当且仅当x=y=![]() 时取等号. ∴三棱锥A-BCD的侧面积的最大值为
时取等号. ∴三棱锥A-BCD的侧面积的最大值为![]() .故选A.
.故选A.


科目:高中数学 来源: 题型:
【题目】2019年电商“双十一”大战即将开始.某电商为了尽快占领市场,抢占今年“双十一”的先机,对成都地区年龄在15到75岁的人群“是否网上购物”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用网上购物的人数如下所示:(年龄单位:岁)
年龄段 |
|
|
|
|
|
|
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
购物人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | 总计 | |
使用网上购物 | |||
不使用网上购物 | |||
总计 |
(2)若从年龄在![]() 的样本中随机选取2人进行座谈,求选中的2人中恰好有1人“使用网上购物”的概率.
的样本中随机选取2人进行座谈,求选中的2人中恰好有1人“使用网上购物”的概率.
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,不同进制之间可以相互转化,例如把十进制的89转化为二进制,根据二进制数“满二进一”的原则,可以用2连续去除89得商,然后取余数,具体计算方法如下:
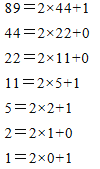
把以上各步所得余数从下到上排列,得到89=1011001(2)这种算法叫做“除二取余法”,上述方法也可以推广为把十进制数化为k进制数的方法,称为“除k取余法”,那么用“除k取余法”把89化为七进制数为_.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月![]() ,
,![]() 两种移动支付方式的使用情况,从全校学生随机抽取了100人,发现使用
两种移动支付方式的使用情况,从全校学生随机抽取了100人,发现使用![]() 或
或![]() 支付方式的学生共有90人,使用
支付方式的学生共有90人,使用![]() 支付方式的学生共有70人,
支付方式的学生共有70人,![]() ,
,![]() 两种支付方式都使用的有60人,则该校使用
两种支付方式都使用的有60人,则该校使用![]() 支付方式的学生人数与该校学生总数比值的估计值为______.
支付方式的学生人数与该校学生总数比值的估计值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在50个不同地区的零售价格全部介于13元与18元之间,将各地价格按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,……,第五组
,……,第五组![]() .如图是按上述分组方法得到的频率分布直方图.
.如图是按上述分组方法得到的频率分布直方图.
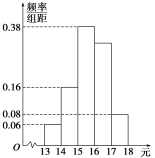
(1)求价格落在![]() 内的地区数;
内的地区数;
(2)借助频率分布直方图,估计该商品价格的中位数(精确到0.1);
(3)现从![]() ,
,![]() 这两组的全部样本数据中,随机选取两个地区的零售价格,记为
这两组的全部样本数据中,随机选取两个地区的零售价格,记为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com