
【题目】某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.

(1)求进入决赛的人数;
(2)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在8.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2-2mx-4my+5m2-4=0(m∈R),圆C2:x2+y2=1.
(1)过定点M(1,-2)作圆C2的切线,求切线的方程;
(2)若圆C1与圆C2相交,求m的取值范围;
(3)已知点P(2,0),圆C1上一点A,圆C2上一点B,求|![]() |的最小值的取值范围.
|的最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中,将底面为直角三角形且侧棱垂直于底面的三棱柱称之为堑堵;将底面为矩形且一侧棱垂直于底面的四棱锥称之为阳马;将四个面均为直角三角形的四面体称之为鳖臑[biē nào].某学校科学小组为了节约材料,拟依托校园内垂直的两面墙和地面搭建一个堑堵形的封闭的实验室![]() ,
,![]() 是边长为2的正方形.
是边长为2的正方形.

(1)若![]() ,
,![]() 在
在![]() 上,四面体
上,四面体![]() 是否为鳖臑,若是,写出其每个面的直角:若不是,请说明理由;
是否为鳖臑,若是,写出其每个面的直角:若不是,请说明理由;
(2)当阳马![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为方便金湖县人民游览三河风景区附近的“网红桥”,现准备在河岸一侧建造一个观景台A,已知射线PM, PN为两边夹角为120°的公路(长度均超过5千米),在两条公路PM,PN上分别设立游客上下点B、C,在观景台A和游客上下点B、C之间和游客上下点B、C之间分别建造三条观光线路AB,AC,BC,测得PB=3干米,PC=5千米.

(1)求线段BC的长度;
(2)若∠BAC= 60°,因政府要计算修建三条观光线路所需费用,所以要计算AB,AC,BC三条线路的总长度的取值范围,请你建立合适的数学模型,帮助政府解决这个问题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面半径为![]() ,母线长为
,母线长为![]() 的圆柱的轴截面是四边形
的圆柱的轴截面是四边形![]() ,线段
,线段![]() 上的两动点
上的两动点![]() ,
, ![]() 满足
满足![]() .点
.点![]() 在底面圆
在底面圆![]() 上,且
上,且![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)四棱锥![]() 的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x-x2)ex-1.
(1)求函数f(x)的单调区间;
(2)若对任意x≥1,都有f(x)-mx-1+m≤0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是两条不同直线,
是两条不同直线,![]() ,
,![]() 是两个不同平面,则下列命题正确的是 ( )
是两个不同平面,则下列命题正确的是 ( )
A. 若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B. 若![]() ,则
,则![]()
C. 若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D. 若![]() ,
,![]() 不平行,则
不平行,则![]() 与
与![]() 不可能垂直于同一平面
不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,得到如图的频率分布直方图(图1).

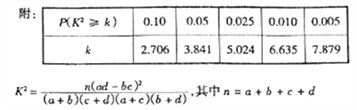
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到图2中数据,根据表中的数据,能否在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com