
����Ŀ��ͨ����������������С�ij߶�������������㹫ʽΪ��![]() �����У�
������![]() �DZ���������������
�DZ���������������![]() �ǡ������𡱵������ʹ�ñ����������Ϊ�����������Ǿ�ʵ�����еľ�����ɵ�ƫ������
�ǡ������𡱵������ʹ�ñ����������Ϊ�����������Ǿ�ʵ�����еľ�����ɵ�ƫ������
��1��������һ�ε����У�һ����������100ǧ���IJ����Ǽ�¼�ĵ�����������30����ʱ������������0��001��������ε����������ȷ��0��1����
��2��5��������˵�����ѱȽ����ԣ�����8���������������5��������������Ķ��ٱ���
���������ݹ��ο���![]() ��
�� ![]() ��
��
���𰸡���1��4��5��2��1000
��������
�����������1�����������ͱ����ֱ�Ӵ��빫ʽM=lgA-lg![]() ��⣻��2�����ö���ʽ��ָ��ʽ�Ļ�����M=lgA-lg
��⣻��2�����ö���ʽ��ָ��ʽ�Ļ�����M=lgA-lg![]() ��A��
��A��![]() ����M=8��M=5�ֱ���빫ʽ���Ⱥɵõ���
����M=8��M=5�ֱ���빫ʽ���Ⱥɵõ���
�����������1��![]()
![]()
��ˣ���ε������Ϊ����4��5����
��2����![]() �ɵ�
�ɵ�![]() ,��
,��![]() ��
��![]() ��
��
��![]() ʱ,�����������Ϊ
ʱ,�����������Ϊ![]() ;��
;��![]() ʱ,�����������Ϊ
ʱ,�����������Ϊ![]() ;���ԣ����ε����������֮���ǣ�
;���ԣ����ε����������֮���ǣ�![]()
��8���������������5���������������1000����


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ׯ����һ���ǵ�Բ������ˮ��(���ƺ��)�������ˮ�صĵ���뾶Ϊr�ף���Ϊh�ף����ΪV�����ף����轨��ɱ����������йأ�����Ľ���ɱ�Ϊ100Ԫ/ƽ���ף�����Ľ���ɱ�Ϊ160Ԫ/ƽ���ף�����ˮ�ص��ܽ���ɱ�Ϊ12 000��Ԫ(��ΪԲ����)��
(1)��V��ʾ��r�ĺ���V(r)������ú����Ķ�����
(2)���ۺ���V(r)�ĵ����ԣ���ȷ��r��hΪ��ֵʱ����ˮ�ص�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ����⣺
![]() ��һ��ƽ���ڵ�����ֱ������һ��ƽ�涼ƽ�У���ô������ƽ���ƽ�У�
��һ��ƽ���ڵ�����ֱ������һ��ƽ�涼ƽ�У���ô������ƽ���ƽ�У�
![]() ��һ��ƽ�澭����һ��ƽ��Ĵ��ߣ���ô������ƽ�����ֱ��
��һ��ƽ�澭����һ��ƽ��Ĵ��ߣ���ô������ƽ�����ֱ��
![]() ��ֱ��ͬһֱ�ߵ�����ֱ���ƽ�У�
��ֱ��ͬһֱ�ߵ�����ֱ���ƽ�У�
![]() ������ƽ�洹ֱ����ôһ��ƽ���������ǵĽ��߲���ֱ��ֱ������һ��ƽ��Ҳ����ֱ��
������ƽ�洹ֱ����ôһ��ƽ���������ǵĽ��߲���ֱ��ֱ������һ��ƽ��Ҳ����ֱ��
���У�Ϊ���������![]() ����
����![]()
A. ![]() ��
��![]() B.
B. ![]() ��
��![]() C.
C. ![]() ��
��![]() D.
D. ![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���֪��A��5����2����B��7,3�����ұ�AC���е�M��y���ϣ���BC���е�N��x���ϣ���
��1������C�����ꣻ
��2��ֱ��MN�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��
��![]() ��ͼ�����ƶ�ʱ����
��ͼ�����ƶ�ʱ����![]() �ں���
�ں���![]() ��ͼ�����ƶ���
��ͼ�����ƶ���
��1������![]() ������Ϊ
������Ϊ![]() ����
����![]() Ҳ��
Ҳ��![]() ͼ���ϣ���
ͼ���ϣ���![]() ��ֵ��
��ֵ��
��2������![]() �Ľ���ʽ��
�Ľ���ʽ��
��3����![]() ����
����![]() ����
����![]() ��
��![]() �ϵ���ֵ��
�ϵ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��![]() ��������Ϊ
��������Ϊ![]() ���ҹ���P��3��2����
���ҹ���P��3��2����
��1������ԲC`�ı����̣�
��2������ֱ��OP��OΪ����ԭ�㣩ƽ�е�ֱ��![]() ����ԲC��A��B���㣬��֤��ֱ��PA��PB��
����ԲC��A��B���㣬��֤��ֱ��PA��PB��![]() ��Χ��һ�����������Σ�
��Χ��һ�����������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ��ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���ᣬ����������ϵȡ��ȵij��ȵ�λ��������ϵ.��ֱ֪��
���������Ϊ���ᣬ����������ϵȡ��ȵij��ȵ�λ��������ϵ.��ֱ֪��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ������
������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������.
������.
��1��������![]() ����ͨ���̺�ֱ��
����ͨ���̺�ֱ��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2��ֱ��![]() ����һ��
����һ��![]() ����ֱ��
����ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�PA�͵���ABCD��AD��AB��AB��DC��AD=DC=AP=2��AB=1����EΪ��PC���е㣮 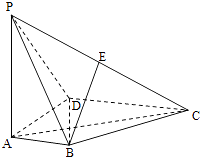
��1��֤����BE��DC��
��2����ֱ��BE��ƽ��PBD���ɽǵ�����ֵ��
��3����FΪ��PC��һ�㣬����BF��AC��������F��AB��P������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com