
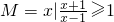 ,集合N={x|2x+3>0},则(CRM)∩N=
,集合N={x|2x+3>0},则(CRM)∩N=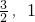 )
)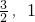 )
)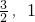 ]
]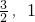 ]
]科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试、理科数学(北京卷) 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合M={![]() },集合N={ x|lg(3-x)>0},则
},集合N={ x|lg(3-x)>0},则![]() =( )
=( )
(A).{ x|2<x<3} (B). { x|1<x<3} (C) . { x|1<x<2} (D) ![]()
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省德州市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知集合 ,集合N={
,集合N={ },则M
},则M N为
N为
A.(-2,3) B.(-3,-2] C.[-2,2) D.(-3,3]
查看答案和解析>>
科目:高中数学 来源:2011年广东省中山市镇区五校高一上学期期中联考数学试卷 题型:选择题
已知集合M={ },集合N={
},集合N={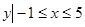 },则M
},则M (
).
(
).
(A){ }
(B){
}
(B){ }
}
(C){ }
(D)
}
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com