
【题目】已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点. 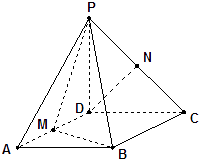
(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)求点A到平面PMB的距离.
【答案】
(1)证明:取PB中点Q,连接MQ、NQ,
因为M、N分别是棱AD、PC中点,
所以QN∥BC∥MD,且QN=MD,于是DN∥MQ.
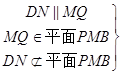 DN∥平面PMB
DN∥平面PMB
(2)解:  PD⊥MB
PD⊥MB
又因为底面ABCD是∠A=60°、边长为a的菱形,且M为AD中点,
所以MB⊥AD.
又AD∩PD=D,
所以MB⊥平面PAD. ![]() 平面PMB⊥平面PAD
平面PMB⊥平面PAD
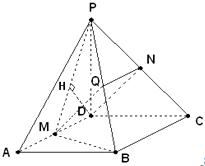
(3)解:因为M是AD中点,所以点A与D到平面PMB等距离.
过点D作DH⊥PM于H,由(2)平面PMB⊥平面PAD,所以DH⊥平面PMB.
故DH是点D到平面PMB的距离. 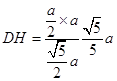 .
.
∴点A到平面PMB的距离为 ![]() .
.
【解析】(1)取PB中点Q,连接MQ、NQ,再加上QN∥BC∥MD,且QN=MD,于是DN∥MQ,再利用直线与平面平行的判定定理进行证明,即可解决问题;(2)易证PD⊥MB,又因为底面ABCD是∠A=60°、边长为a的菱形,且M为AD中点,然后利用平面与平面垂直的判定定理进行证明;(3)因为M是AD中点,所以点A与D到平面PMB等距离,过点D作DH⊥PM于H,由(2)平面PMB⊥平面PAD,所以DH⊥平面PMB,DH是点D到平面PMB的距离,从而求解.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜” 
(1)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
(2)将频率视为概率,现在从该校大量学生中,用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中的“读书谜”的人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方程D(X) 附:K2= ![]() n=a+b+c+d
n=a+b+c+d
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a,b,c,且a>c,已知 ![]()
![]() =2,cosB=
=2,cosB= ![]() ,b=3,求:
,b=3,求:
(Ⅰ)a和c的值;
(Ⅱ)cos(B﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将直线2x﹣y+λ=0沿x轴向左平移1个单位,所得直线与圆x2+y2+2x﹣4y=0相切,则实数λ的值为( )
A.﹣3或7
B.﹣2或8
C.0或10
D.1或11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,已知A(﹣2,0),直角顶点B(0,﹣2 ![]() ),点C在x轴上.
),点C在x轴上. 
(Ⅰ)求Rt△ABC外接圆的方程;
(Ⅱ)求过点(﹣4,0)且与Rt△ABC外接圆相切的直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax﹣f(x)(a>0且a≠1),其中f(x)是定义在[a﹣6,2a]上的奇函数,若 ![]() ,则g(1)=( )
,则g(1)=( )
A.0
B.﹣3
C.1
D.﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com