练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】经过对K2的统计量的研究，得到了若干个观测值，当K2≈6.706时，我们认为两分类变量A、B(　　)

    A. 有67.06%的把握认为A与B有关系 B. 有99%的把握认为A与B有关系

    C. 有0.010的把握认为A与B有关系 D. 没有充分理由说明A与B有关系

    【答案】B

    【解析】

    根据所给的观测值，同临界值表中的临界值进行比较，根据P（K2＞3.841）=0.05，得到我们有1-0.05=95%的把握认为A与B有关系．

    依据下表：

    P（ K2≥k）

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    ，

    ∴我们在错误的概率不超过0.01的前提下有99%的把握认为A与B有关系，
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=1+x﹣ + ﹣ ﹣…+ ﹣ + ，则下列结论正确的是（ ）
    A.f（x）在（0，1）上恰有一个零点
    B.f（x）在（0，1）上恰有两个零点
    C.f（x）在（﹣1，0）上恰有一个零点
    D.f（x）在（﹣1，0）上恰有两个零点

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以平面直角坐标系原点O为极点，以x轴非负半轴为极轴，以平面直角坐标系的长度单位为长度单位建立极坐标系．已知直线l的参数方程为 （t为参数），曲线C的极坐标方程为ρsin2θ=4cosθ
    （Ⅰ） 求曲线C的直角坐标方程；
    （Ⅱ） 设直线l与曲线C相交于A，B两点，求|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设a＞0，b＞0（ ）
    A.若lna+2a=lnb+3b，则a＞b
    B.2a+2a=2b+3b，则a＜b
    C.若lna﹣2a=lnb﹣3b，则a＞b
    D.2a﹣2a=2b﹣3b，则a＜b

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= sinωxcosωx﹣cos2ωx﹣ （ω＞0，x∈R）的图象上相邻两个最高点的距离为π．
    （Ⅰ）求函数f（x）的单调递增区间；
    （Ⅱ）若△ABC三个内角A、B、C的对边分别为a、b、c，且c= ，f（C）=0，sinB=3sinA，求a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设不等式|2x﹣1|＜1的解集为M，a∈M，b∈M
    （1）试比较ab+1与a+b的大小
    （2）设max表示数集A的最大数，h=max{ ， ， }，求证h≥2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若图所示，将若干个点摆成三角形图案，每条边（包括两个端点）n（n＞1，n∈N*）个点，相应的图案中总的点数记为an ， 则 + + +…+ = ．

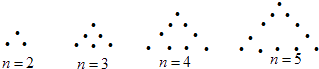
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将一颗骰子先后抛掷2次，观察向上的点数，求：

    (1)两数之和为5的概率；

    (2)两数中至少有一个奇数的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=sinωx+cosωx的最小正周期为π，x∈R，ω＞0是常数．
    （1）求ω的值；
    （2）若f（+）= ， θ∈（0，），求sin2θ．

    查看答案和解析>>

    同步练习册答案