
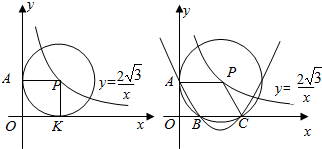 在直角坐标系xOy中,已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
在直角坐标系xOy中,已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.分析 (1)先证四边形OKPA为矩形,再根据AP=KP,得出四边形OKPA是正方形;
(2)①先根据几何关系得出△PBC为等边三角形,再求出P点坐标,进而得出A,B,C的坐标;
②先设出二次函数的解析式,求出直线BP的解析式,并根据面积求出直线AM的解析式,最后联立方程求M的坐标.
解答 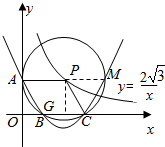 解:(1)四边形OKPA是正方形,证明如下:
解:(1)四边形OKPA是正方形,证明如下:
∵⊙P分别与两坐标轴相切,
∴PA⊥OA,PK⊥OK.∴∠PAO=∠OKP=90°,
又∵∠AOK=90°,∴∠PAO=∠OKP=∠AOK=90°,
∴四边形OKPA是矩形,
又∵AP=KP,∴四边形OKPA是正方形.
(2)①连接PB,过点P作PG⊥BC于G,
∵四边形ABCP为菱形,∴BC=PA=PB=PC(半径),
∴△PBC为等边三角形,
在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=$\frac{{\sqrt{3}}}{2}x$
∴P(x,$\frac{\sqrt{3}}{2}$x)代入$y=\frac{{2\sqrt{3}}}{x}$,解之得:x=±2(负值舍去).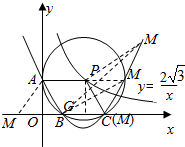
∴PG=$\sqrt{3}$,PA=BC=2,则P(2,$\sqrt{3}$),
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3.
∴A(0,$\sqrt{3}$),B(1,0),C(3,0).
②设二次函数解析式为:y=a(x-1)(x-3),过点A(0,$\sqrt{3}$),
∴$a=\frac{{\sqrt{3}}}{3}$,∴二次函数解析式为:y=$\frac{{\sqrt{3}}}{3}$x2-$\frac{{4\sqrt{3}}}{3}$x+$\sqrt{3}$
设直线BP的解析式为:y=ux+v,
据题意得:$\left\{\begin{array}{l}u+v=0\\ 2u+v=\sqrt{3}\end{array}\right.$解之得:$\left\{\begin{array}{l}u=\sqrt{3}\\ v=-\sqrt{3}\end{array}\right.$.
∴直线BP的解析式为:y=$\sqrt{3}$x-$\sqrt{3}$,
要使${S_{△MBP}}=\frac{1}{2}{S_{菱形ABCP}}={S_{ABP}}={S_{△CBP}}$,
过点A作直线AM∥BP,则可得直线AM的解析式为:y=$\sqrt{3}$x+$\sqrt{3}$,
解方程组:$\left\{\begin{array}{l}y=\sqrt{3}x+\sqrt{3}\\ y=\frac{{\sqrt{3}}}{3}{x^2}-\frac{{4\sqrt{3}}}{3}x+\sqrt{3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x_1}=0\\{y_1}=\sqrt{3}\end{array}\right.$或$\left\{\begin{array}{l}{x_2}=7\\{y_2}=8\sqrt{3}\end{array}\right.$,
过点C作直线CM∥PB,则可设直线CM的解析式为:y=$\sqrt{3}$x+t,
∴0=3$\sqrt{3}$+t,∴t=-3$\sqrt{3}$,
∴直线CM的解析式为:y=$\sqrt{3}$x-3$\sqrt{3}$,
解方程组:$\left\{\begin{array}{l}y=\sqrt{3}x-3\sqrt{3}\\ y=\frac{{\sqrt{3}}}{3}x2-\frac{{4\sqrt{3}}}{3}x+\sqrt{3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x_1}=3\\{y_1}=0\end{array}\right.$;$\left\{\begin{array}{l}{x_2}=4\\{y_2}=\sqrt{3}\end{array}\right.$,
综上可知,满足条件的M的坐标有四个,
分别为:(0,$\sqrt{3}$),(3,0),(4,$\sqrt{3}$),(7,8$\sqrt{3}$).
点评 本题主要考查了函数解析式的求法,圆的性质的综合应用,四边形形状的判断和菱形的面积的求解,体现了数形结合的解题思想,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P(B)=$\frac{2}{5}$ | |
| B. | 事件B与事件A1相互独立 | |
| C. | P(B|A1)=$\frac{5}{11}$ | |
| D. | P(B)的值不能确定,它与A1,A2,A3中哪一个发生都有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | -$\frac{1}{7}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com