
【题目】已知二次函数f(x)=ax2+bx﹣3在x=1处取得极值,且在(0,﹣3)点处的切线与直线2x+y=0平行. (Ⅰ)求f(x)的解析式;
(Ⅱ)求函数g(x)=xf(x)+4x的单调递增区间.
【答案】解:(Ⅰ)由f(x)=ax2+bx﹣3,可得f′(x)=2ax+b. 由题设可得 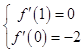 即
即 ![]()
解得a=1,b=﹣2.
所以f(x)=x2﹣2x﹣3.
(Ⅱ)由题意得g(x)=xf(x)+4x=x3﹣2x2+x,
所以g′(x)=3x2﹣4x+1=(3x﹣1)(x﹣1).
令g′(x)=0,得 ![]() ,x2=1.
,x2=1. 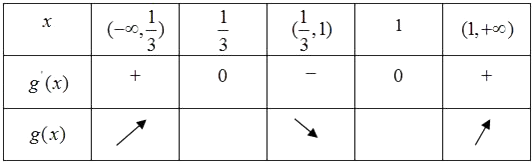
所以函数g(x)的单调递增区间为 ![]() ,(1,+∞)
,(1,+∞)
【解析】(Ⅰ)先对函数f(x)求导,令f'(1)=0,f'(0)=﹣2即可得到答案.(Ⅱ)将函数f(x)的解析式代入求出函数g(x)的解析式后求导,令导函数大于0求出x的范围即可.
【考点精析】利用导数的几何意义和利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间
;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】请阅读下列材料:若两个正实数a1 , a2满足a12+a22=1,那么a1+a2 ![]() .证明:构造函数f(x)=(x﹣a1)2+(x﹣a2)2=2x2﹣2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以△≤0,从而得4(a1+a2)2﹣8≤0,所以a1+a2
.证明:构造函数f(x)=(x﹣a1)2+(x﹣a2)2=2x2﹣2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以△≤0,从而得4(a1+a2)2﹣8≤0,所以a1+a2 ![]() .根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为 .
.根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面使用类比推理正确的是( )
A.直线a∥b,b∥c,则a∥c,类推出:向量 ![]() ,
, ![]() ,则
,则 ![]()
B.同一平面内,直线a,b,c,若a⊥c,b⊥c,则a∥b.类推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b
C.实数a,b,若方程x2+ax+b=0有实数根,则a2≥4b.类推出:复数a,b,若方程x2+ax+b=0有实数根,则a2≥4b
D.以点(0,0)为圆心,r为半径的圆的方程为x2+y2=r2 . 类推出:以点(0,0,0)为球心,r为半径的球的方程为x2+y2+z2=r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字). 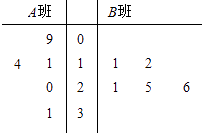
(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(Ⅱ)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣(a+2)x+lnx. (Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当a>0时,若f(x)在区间[1,e]上的最小值为﹣2,求a的取值范围;
(Ⅲ)若对任意x1 , x2∈(0,+∞),当x1≠x2时有 ![]() >0恒成立,求a的取值范围.
>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一次函数f(x)在R上单调递增,当x∈[0,3]时,值域为[1,4].
(1)求函数f(x)的解析式;
(2)当x∈[﹣1,8]时,求函数 ![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com