
分析 先设买A胶合板x张,B胶合板y张,付出资金z元,根据题意抽象出x,y满足的条件,建立约束条件,作出可行域,再根据目标函数z=40x+16y,利用截距模型,平移直线找到最优解即可
解答 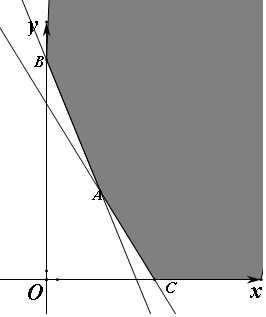 解:(1)买A胶合板x张,B胶合板y张,由题意得到$\left\{\begin{array}{l}{2x+y≥20}\\{6x+2y≥50}\\{x≥0}\\{y≥0}\\{x,y∈N}\end{array}\right.$,平面区域如图:
解:(1)买A胶合板x张,B胶合板y张,由题意得到$\left\{\begin{array}{l}{2x+y≥20}\\{6x+2y≥50}\\{x≥0}\\{y≥0}\\{x,y∈N}\end{array}\right.$,平面区域如图:
(2)设花费资金z=200x+72y,由(1)$\left\{\begin{array}{l}{2x+y=20}\\{6x+2y=50}\end{array}\right.$得A(5,10).
由图可知当x=5,y=10时.zmin=1000+720=1720(元)
答:买A型木板5张,B型木板10张,付出资金最少为1720元.
点评 本题主要考查用线性规划解决实际问题中的最值问题,基本思路是抽象约束条件,作出可行域,利用目标函数的类型,找到最优解.属中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{32}{3}$ | B. | 8 | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
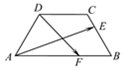 如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )| A. | λ∈($\frac{1}{8}$,$\frac{1}{4}$) | B. | λ∈($\frac{1}{4}$,$\frac{3}{8}$) | C. | λ∈($\frac{3}{8}$,$\frac{1}{2}$) | D. | λ∈($\frac{1}{2}$,$\frac{5}{8}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{6}$ | B. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{6}$ | ||
| C. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{12}$ | D. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
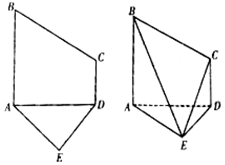 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com