
 如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径$r=\root{3}{10}$毫米,滴管内液体忽略不计.如果瓶内的药液恰好156分钟滴完,则每分钟应滴下75滴.
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径$r=\root{3}{10}$毫米,滴管内液体忽略不计.如果瓶内的药液恰好156分钟滴完,则每分钟应滴下75滴. 分析 设每分钟滴下k(k∈N*)滴,由圆柱的体积公式求出瓶内液体的体积,再求出k滴球状液体的体积,得到156分钟所滴液体体积,由体积相等得到k的值.
解答 解:设每分钟滴下k(k∈N*)滴,
则瓶内液体的体积${V}_{1}=π•{4}^{2}•9+π•{2}^{2}•3$=156πcm3,
k滴球状液体的体积${V}_{2}=k•\frac{4}{3}π•10$=$\frac{40}{3}kπ$mm3=$\frac{kπ}{75}$cm3,
∴156π=$\frac{kπ}{75}$×156,解得k=75,
故每分钟应滴下75滴.
故答案为:75.
点评 本题考查简单的数学建模思想方法,解答的关键是对题意的理解,然后正确列出体积相等的关系式,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
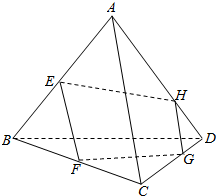 如图,ABCD为空间四边形,点E,F分别是AB,BC的中点,点G,H分别在CD,AD上,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$CD.
如图,ABCD为空间四边形,点E,F分别是AB,BC的中点,点G,H分别在CD,AD上,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 2($\sqrt{3}$+1) | D. | 2($\sqrt{3}$-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com