
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,判断
时,判断![]() 的单调性;
的单调性;
(2)若函数![]() 无零点,求a的取值范围.
无零点,求a的取值范围.
【答案】(1)在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减(2)
上单调递减(2)![]()
【解析】
(1)先求导数,再求导函数零点,根据零点讨论导函数符号变化规律,即得函数单调性;
(2)先根据![]() 且函数
且函数![]() 无零点,得
无零点,得![]() 恒成立,方法一:对
恒成立,方法一:对![]() 分类讨论并参变分离,转化为求对应函数最值,再根据导数求对应函数最值,即可得结果;方法二:转化研究
分类讨论并参变分离,转化为求对应函数最值,再根据导数求对应函数最值,即可得结果;方法二:转化研究![]() 单调性,对
单调性,对![]() 分类讨论,结合单调性确定
分类讨论,结合单调性确定![]() 最值,即得结果.
最值,即得结果.
解:(1)当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() 得
得![]() ;令
;令![]() 得
得![]() 或
或![]() .
.
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减.
上单调递减.
(2)方法一:因为 ![]() ,且函数
,且函数![]() 无零点,
无零点,
![]() ,
,![]() 成立,即
成立,即![]() 恒成立,
恒成立,
![]() .
.
①当![]() 时,
时,![]() 恒成立,
恒成立,![]() .
.
②当![]() 时,
时,![]() ,令
,令![]() ,则
,则![]() ,
,
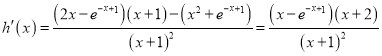 ,
,
又![]() 在
在![]() 上单调递增,且
上单调递增,且![]() 时,
时,![]() ,
,
令![]() 得
得![]() ,
,![]() ,
,
x |
| 1 |
|
|
| 0 |
|
| 单调递减 | 极小值 | 单调递增 |
![]() ,
,![]() .
.
③当![]() 时,
时,![]() ,则
,则![]() .
.
又![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
令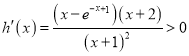 得
得![]() ,即
,即![]() ,
,
x |
|
|
|
|
| 0 |
|
| 单调递增 | 极大值 | 单调递减 |
![]() ,
,![]() .
.
综上,![]() .
.
方法二:因为![]() ,且函数
,且函数![]() 无零点,
无零点,
![]() ,
,![]() 成立,即
成立,即![]() 恒成立,
恒成立,
![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
而![]() ,
,
①当![]() 时,
时,![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() 的极大值为
的极大值为![]() ,
,
![]() 恒成立,即极大值
恒成立,即极大值![]() 且当
且当![]() 时,
时,![]() .
.
(i)若![]() ,且
,且 ![]() 在
在![]() 单调递增,
单调递增,
有![]() ,
,
此时![]() 成立.
成立.
(ii)由![]() 得
得![]() ,
,
②当![]() 时,
时,![]() 成立.
成立.
③当![]() 时,
时,![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() 的极大值为
的极大值为![]() ,
,
![]() 恒成立,即极大值
恒成立,即极大值![]() 且当
且当![]() 时,
时,![]() .
.
(i)若![]() ,因为
,因为![]() 在
在![]() 单调递增,且
单调递增,且![]() ,
,
有![]() ,
,
此时![]() 成立.
成立.
(ii)由![]() 得
得![]() .
.
综上,![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂生产的10件产品中,有8件合格品、2件不合格品,合格品与不合格品在外观上没有区别.从这10件产品中任意抽检2件,计算:
(1)2件都是合格品的概率;
(2)1件是合格品、1件是不合格品的概率;
(3)如果抽检的2件产品都是不合格品,那么这批产品将被退货,求这批产品被退货的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为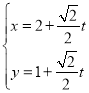 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() ,
,![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆O:x2+y2=8内有一点P(﹣1,2),AB为过点P且倾斜角为α的弦,
(1)当α=135°时,求AB的长;
(2)当弦AB被点P平分时,写出直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省即将实行新高考,不再实行文理分科.某校研究数学成绩优秀是否对选择物理有影响,对该校2018级的500名学生进行调在收集到相关数据如下:
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 130 | ||
总计 | 300 | 500 |

(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: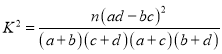 .
.
临界值表:
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员每场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据被墨迹污损不清(如图1),但甲得分的折线图完好(如图2),则下列结论错误的是( )
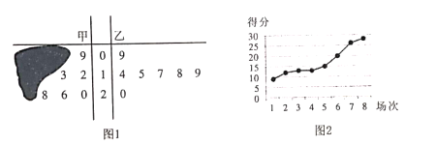
A.乙运动员得分的中位数是17,甲运动员得分的极差是19
B.甲运动员发挥的稳定性比乙运动员发挥的稳定性差
C.甲运动员得分有![]() 的叶集中在茎1上
的叶集中在茎1上
D.甲运动员得分的平均值一定比乙运动员得分的平均值低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y万元有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
附注:①参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com