|
|
|
已知函数f(x)=2x3-3x.
(1)求f(x)在区间[-2,1]上的最大值;
(2)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;
(3)问过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
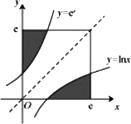
如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则他落到阴影部分的概率为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.咋特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系p=at2+bt+c(a、b、c是常数),下图
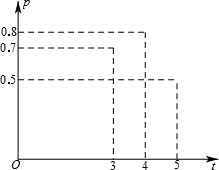
记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为
|
| [ ] |
A. |
3.50分钟
|
B. |
3.75分钟
|
C. |
4.00分钟
|
D. |
4.25分钟
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设{an}是公比为q的等比数列,则“q>1”是“{an}”为递增数列的
|
| [ ] |
A. |
充分且不必要条件
|
B. |
必要且不充分条件
|
C. |
充分必要条件
|
D. |
既不充分也不必要条件
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若等差数列{an}满足a7+a8+a9>0,a7+a10<0,则当n=________时{an}的前n项和最大.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数f(x)=|x+1|+|2x+a|的最小值3,则实数a的值为
|
| [ ] |
A. |
5或8
|
B. |
-1或5
|
C. |
-1或-4
|
D. |
-4或8
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数.给出四个函数f1(x)=2log2x,f2(x)=log2(x+2),f3(x)=(log2x)2,f4(x)=log2(2x),则“同形”函数是
|
| [ ] |
A. |
f1(x)与f2(x)
|
B. |
f2(x)与f3(x)
|
C. |
f1(x)与f4(x)
|
D. |
f2(x)与f4(x)
|
|
|
查看答案和解析>>

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案