
【题目】某蛋糕店每天做若干个生日蛋糕,每个制作成本为50元,当天以每个100元售出,若当天白天售不出,则当晚以30元/个价格作普通蛋糕低价售出,可以全部售完.
(1)若蛋糕店每天做20个生日蛋糕,求当天的利润![]() (单位:元)关于当天生日蛋糕的需求量
(单位:元)关于当天生日蛋糕的需求量![]() (单位:个,
(单位:个, ![]() )的函数关系;
)的函数关系;
(2)蛋糕店记录了100天生日蛋糕的日需求量(单位:个)整理得下表:

(ⅰ)假设蛋糕店在这100天内每天制作20个生日蛋糕,求这100天的日利润(单位:元)的平均数;
(ⅱ)若蛋糕店一天制作20个生日蛋糕,以100天记录的各需求量的频率作为概率,求当天利润不少于900元的概率.
科目:高中数学 来源: 题型:
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下2×2的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式![]() ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确是( )
A. 有![]() 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”
B. 有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
C. 有![]() 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”
D. 有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,底面
中,底面![]() 为正三角形,
为正三角形, ![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
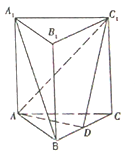
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得三棱锥
,使得三棱锥![]() 的体积是
的体积是![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差大于零的等差数列{an}的前n项和为Sn , 且满足a3a4=117,a2+a5=22.
(1)求通项an;
(2)若数列{bn}满足bn= ![]() ,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com