
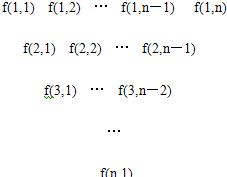 һ�����������������·�ʽ���ɣ���һ������д��n��n��4������������һ�е�ÿ�����������м����·�д��������֮�ͣ��õ���һ�У��������ƣ��������е�i�еĵ�j����Ϊf��i��j����
һ�����������������·�ʽ���ɣ���һ������д��n��n��4������������һ�е�ÿ�����������м����·�д��������֮�ͣ��õ���һ�У��������ƣ��������е�i�еĵ�j����Ϊf��i��j����| 1 |
| aiai+1 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| f(i��1) |
| i+1 |
| 1 |
| aiai+1 |
| 1 |
| (2i+1)(2i+1+1) |
| 1 |
| 2i |
| 1 |
| 2i+1 |
| 1 |
| 2i+1+1 |
| 1 |
| 2i+1 |
| 1 |
| 2i+1+1 |
| 1 |
| 3 |
| 1 |
| 2n+1+1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2n+1+1 |
| 1 |
| 2n+1+1 |
| 1 |
| 3 |
| 1-3m |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 1-3m |
| 3 |
| 1-3m |
| 3 |
| 1-3m |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2010��������ѧ��һ��ѧ����ĩ������ѧ ���ͣ������
����С������16�֣� һ�����������������·�ʽ���ɣ���һ������д��n(n��4)����������һ�е�ÿ�����������м����·�д��������֮�ͣ��õ���һ�У��������ƣ��������е�i�еĵ�j����Ϊf(i,j)��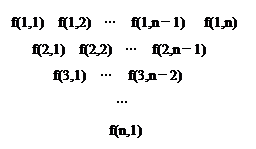
(1)�������е�i (1��i��n��3)�е������γɵȲ����У���֤����i+1�е���Ҳ���γɵȲ����У�
(2)��֪f(1,j)=4j����f(i,1)����i�ı���ʽ��
(3)��(2)�������£���f(i,1)=(i+1)(ai��1)��bi= ������һ������g(x)��ʹ��
Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�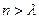 ʱ������Sn >m.
ʱ������Sn >m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010��������ѧ��һ��ѧ����ĩ������ѧ ���ͣ������
����С������16�֣� һ�����������������·�ʽ���ɣ���һ������д��n(n��4)����������һ�е�ÿ�����������м����·�д��������֮�ͣ��õ���һ�У��������ƣ��������е�i�еĵ�j����Ϊf(i,j)��
(1)�������е�i (1��i��n��3)�е������γɵȲ����У���֤����i+1�е���Ҳ���γɵȲ����У�
(2)��֪f(1,j)=4j����f(i,1)����i�ı���ʽ��
(3)��(2)�������£���f(i,1)=(i+1)(ai��1)��bi= ������һ������g(x)��ʹ��
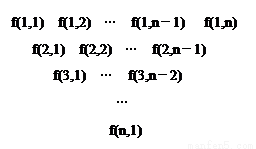 Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�
Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�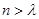 ʱ������Sn >m.
ʱ������Sn >m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������16�֣� һ�����������������·�ʽ���ɣ���һ������д��n(n��4)����������һ�е�ÿ�����������м����·�д��������֮�ͣ��õ���һ�У��������ƣ��������е�i�еĵ�j����Ϊf(i,j)��
(1)�������е�i (1��i��n��3)�е������γɵȲ����У���֤����i+1�е���Ҳ���γɵȲ����У�
(2)��֪f(1,j)=4j����f(i,1)����i�ı���ʽ��
(3)��(2)�������£���f(i,1)=(i+1)(ai��1)��bi= ������һ������g(x)��ʹ��
 Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�n��ʱ������Sn >m.
Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�n��ʱ������Sn >m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2009-2010ѧ�꽭��ʡ������ѧ��һ���£���ĩ��ѧ�Ծ��������棩 ���ͣ������
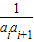 ������һ������f��x����ʹ��Sn=b1g��1��+b2g��2��+��+bng��n����
������һ������f��x����ʹ��Sn=b1g��1��+b2g��2��+��+bng��n���� ���Ҷ��������m�ʣ�
���Ҷ��������m�ʣ� ��
�� ����������ʵ����?��ʹ�õ�n��?��ʱ������Sn��m��
����������ʵ����?��ʹ�õ�n��?��ʱ������Sn��m��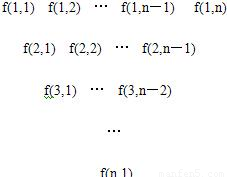
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com