
(本小题满分14分)
已知双曲线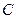 :
: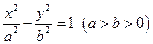 和圆
和圆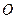 :
: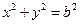 (其中原点
(其中原点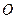 为圆心),过双曲线
为圆心),过双曲线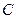 上一点
上一点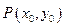 引圆
引圆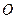 的两条切线,切点分别为
的两条切线,切点分别为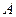 、
、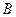 .
.
(1)若双曲线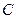 上存在点
上存在点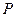 ,使得
,使得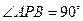 ,求双曲线离心率
,求双曲线离心率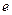 的取值范围;
的取值范围;
(2) 求直线
求直线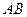 的方程;
的方程;
(3)求三角形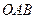 面积的最大值.
面积的最大值.
解:(1)因为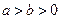 ,所以
,所以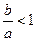 ,所以
,所以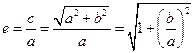
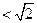 .…………………1分
.…………………1分
由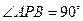 及圆的性质,可知四边形
及圆的性质,可知四边形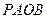 是正方形,所以
是正方形,所以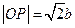 .
.
因为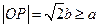 ,所以
,所以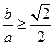 ,所以
,所以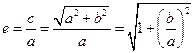
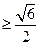 .……………3分
.……………3分
故双曲线离心率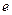 的取值范围为
的取值范围为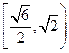 .…………………………………………………………4分
.…………………………………………………………4分
(2)方法1:因为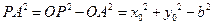 ,
,
所以以点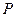 为圆心,
为圆心,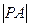 为半径的圆
为半径的圆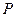 的方程为
的方程为 .………5分
.………5分
因为圆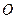 与圆
与圆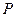 两圆的公共弦所在的直线即为直线
两圆的公共弦所在的直线即为直线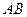 ,……………………………………………6分
,……………………………………………6分
所以联立方程组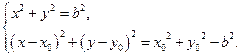 ………………………………………………7分
………………………………………………7分
消去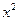 ,
,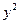 ,即得直线
,即得直线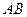 的方程为
的方程为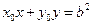 .………………………………………………8分
.………………………………………………8分
方法2:设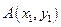
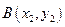 ,已知点
,已知点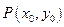 ,
,
则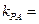
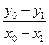 ,
,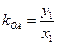
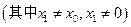 .
.
因为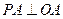 ,所以
,所以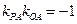 ,即
,即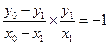 .…………………………………………5分
.…………………………………………5分
整理得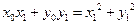 .
.
因为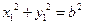 ,所以
,所以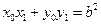 .……………………………………………………………6分
.……………………………………………………………6分
因为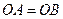 ,
,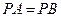 ,根据平面几何知识可知,
,根据平面几何知识可知,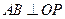 .
.
因为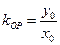 ,所以
,所以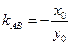 .………………………………………………………………………7分
.………………………………………………………………………7分
所以直线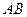 方程为
方程为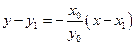 .
.
即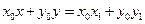 .
.
所以直线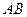 的方程为
的方程为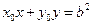 .………………………………………………………………8分
.………………………………………………………………8分
方法3:设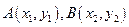 ,已知点
,已知点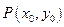 ,
,
则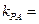
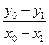 ,
,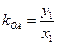
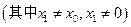 .
.
因为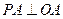 ,所以
,所以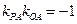 ,即
,即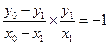 .…………………………………………5分
.…………………………………………5分
整理得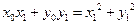 .
.
因为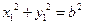 ,所以
,所以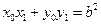 .……6分
.……6分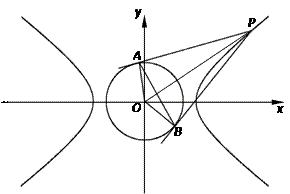
这说明点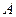 在直线
在直线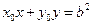 上.…………7分
上.…………7分
同理点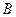 也在直线
也在直线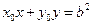 上.
上.
所以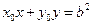 就是直线
就是直线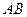 的方程.……8分
的方程.……8分
(3)由(2)知,直线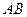 解析
解析


科目:高中数学 来源: 题型:单选题
设双曲线C: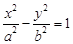 (a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为
(a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为
A.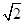 | B.2 | C. | D. 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com