
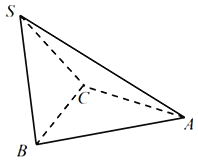
【题目】如图所示,三棱锥S一ABC中,△ABC与△SBC都是边长为1的正三角形,二面角A﹣BC﹣S的大小为![]() ,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
A.![]() πB.
πB.![]() πC.
πC.![]() πD.3π
πD.3π
【答案】A
【解析】
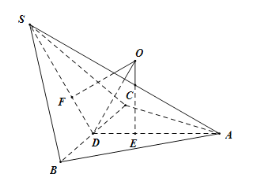
取线段BC的中点D,连结AD,SD,由题意得AD⊥BC,SD⊥BC,∠ADS是二面角A﹣BC﹣S的平面角,∠ADS![]() ,由题意得BC⊥平面ADS,分别取AD,SD的三等分点E,F,在平面ADS内,过点E,F分别作直线垂直于AD,SD,两条直线的交点即球心O,连结OA,则球O半径R=|OA|,由此能求出球O的表面积.
,由题意得BC⊥平面ADS,分别取AD,SD的三等分点E,F,在平面ADS内,过点E,F分别作直线垂直于AD,SD,两条直线的交点即球心O,连结OA,则球O半径R=|OA|,由此能求出球O的表面积.
解:取线段BC的中点D,连结AD,SD,
由题意得AD⊥BC,SD⊥BC,
∴∠ADS是二面角A﹣BC﹣S的平面角,∴∠ADS![]() ,
,
由题意得BC⊥平面ADS,
分别取AD,SD的三等分点E,F,
在平面ADS内,过点E,F分别作直线垂直于AD,SD,
两条直线的交点即球心O,
连结OA,则球O半径R=|OA|,
由题意知BD![]() ,AD
,AD![]() ,DE
,DE![]() ,AE
,AE![]() ,
,
连结OD,在Rt△ODE中,![]() ,OE
,OE![]() DE
DE![]() ,
,
∴OA2=OE2+AE2![]() ,
,
∴球O的表面积为S=4πR2![]() .
.
故选:A.


科目:高中数学 来源: 题型:
【题目】近年来电子商务蓬勃发展,同时也极大地促进了快递行业的发展,为了更好地服务客户,某快递公司使用客户评价系统对快递服务人员的服务进行评价,每月根据客户评价评选出“快递之星”.已知“快递小哥”小张在每个月被评选为“快递之星”的概率都是![]() ,则小张在第一季度的3个月中有2个月都被评为“快递之星”的概率为_______;设小张在上半年的6个月中被评为“快递之星”的次数为随机变量X,则随机变量X的方差
,则小张在第一季度的3个月中有2个月都被评为“快递之星”的概率为_______;设小张在上半年的6个月中被评为“快递之星”的次数为随机变量X,则随机变量X的方差![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 相切于点
相切于点![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)求抛物线![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设![]() 是
是![]() 轴上两个不同的动点,且满足
轴上两个不同的动点,且满足![]() ,直线
,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的另一个交点分别为
的另一个交点分别为![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.如果相交,求出的交点的坐标.
的位置关系,并说明理由.如果相交,求出的交点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,过右焦点
的左、右顶点,过右焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
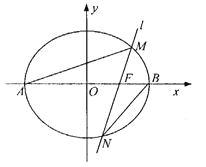
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点下的距离为10.
到其焦点下的距离为10.
(1)求抛物线C的方程;
(2)设过焦点F的的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,且抛物线在
两点,且抛物线在![]() 两点处的切线分别交x轴于
两点处的切线分别交x轴于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为筛查在人群中传染的某种病毒,现有两种检测方法:
(1)抗体检测法:每个个体独立检测,每一次检测成本为80元,每个个体收取检测费为100元.
(2)核酸检测法:先合并个体,其操作方法是:当个体不超过10个时,把所有个体合并在一起进行检测.
当个体超过10个时,每10个个体为一组进行检测.若该组检测结果为阴性(正常),则只需检测一次;若该组检测结果为阳性(不正常),则需再对每个个体按核酸检测法重新独立检测,共需检测k+1次(k为该组个体数,1≤k≤10,k∈N*).每一次检测成本为160元.假设在接受检测的个体中,每个个体的检测结果是阳性还是阴性相互独立,且每个个体是阳性结果的概率均为p(0<p<1).
(Ⅰ)现有100个个体采取抗体检测法,求其中恰有一个检测出为阳性的概率;
(Ⅱ)因大多数人群筛查出现阳性的概率很低,且政府就核酸检测法给子检测机构一定的补贴,故检测机构推出组团选择核酸检测优惠政策如下:无论是检测一次还是k+1次,每组所有个体共收费700元(少于10个个体的组收费金额不变).已知某企业现有员工107人,准备进行全员检测,拟准备9000元检测费,由于时间和设备条件的限制,采用核酸检测法合并个体的组数不得高于参加采用抗体检测法人数,请设计一个合理的的检测安排方案;
(Ⅲ)设![]() ,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年是全面建成小康社会目标实现之年,也是全面打赢脱贫攻坚战收官之年.某乡镇在2014年通过精准识别确定建档立卡的贫困户共有500户,结合当地实际情况采取多项精准扶贫措施,每年新脱贫户数如下表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
脱贫户数 | 55 | 68 | 80 | 92 | 100 |
(1)根据2015-2019年的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测到2020年底该乡镇500户贫困户是否能全部脱贫;
,并预测到2020年底该乡镇500户贫困户是否能全部脱贫;
(2)2019年的新脱贫户中有20户五保户,20户低保户,60户扶贫户.该乡镇某干部打算按照分层抽样的方法对2019年新脱贫户中的5户进行回访,了解生产生活、帮扶工作开展情况.为防止这些脱贫户再度返贫,随机抽取这5户中的2户进行每月跟踪帮扶,求抽取的2户不都是扶贫户的概率.
参考公式: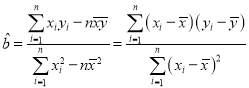 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如表,其中一等奖代表队比三等奖代表队多10人.该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动.并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中二等奖代表队有5人(同队内男女生仍采用分层抽样)
名次 性别 | 一等奖 代表队 | 二等奖 代表队 | 三等奖 代表队 |
男生 | ? | 30 | ◎ |
女生 | 30 | 20 | 30 |
(1)从前排就坐的一等奖代表队中随机抽取3人上台领奖,用X表示女生上台领奖的人数,求X的分布列和数学期望E(X).
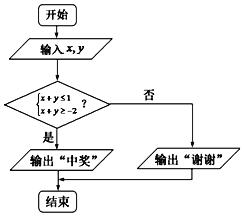
(2)抽奖活动中,代表队员通过操作按键,使电脑自动产生[﹣2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序.若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖.求代表队队员获得奖品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com