
【题目】已知数列{an}的前n项和为Sn,对任意的正整数n,都有Sn=![]() an+n-3成立.
an+n-3成立.
(1)求证:存在实数λ使得数列{an+λ}为等比数列;
(2)求数列{nan}的前n项和Tn.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)先根据和项与通项公式得项之间递推关系an=3an-1-2,再构造an-1=3(an-1-1),由等比数列定义确定结论,(2)因为数列为等差与等比乘积型,所以利用错位相减法求数列{nan}的前n项和Tn.
试题解析:(1)证明:因为Sn=![]() an+n-3,①
an+n-3,①
所以当n=1时,S1=![]() a1+1-3,所以a1=4.
a1+1-3,所以a1=4.
当n≥2时,Sn-1=![]() an-1+n-1-3,②
an-1+n-1-3,②
由①②两式相减得an=![]() an-
an-![]() an-1+1,即
an-1+1,即
an=3an-1-2(n≥2).变形得an-1=3(an-1-1),而a1-1=3,
所以数列{an-1}是首项为3,公比为3的等比数列,
所以存在实数λ=-1,使得数列{an-1}为等比数列.
(2)由(1)得an-1=3·3n-1=3n,
所以an=3n+1,nan=n·3n+n,所以Tn=(1×31+2×32+3×33+…+n×3n)+(1+2+3+…+n),
令Vn=1×31+2×32+3×33+…+n×3n,③
则3Vn=1×32+2×33+3×34+…+n×3n+1,④
由③④两式相减得
-2Vn=3+32+33+…+3n-n×3n+1=![]() -n×3n+1=
-n×3n+1=![]() ·3n+1-
·3n+1-![]() ,
,
所以Vn=![]() ·3n+1+
·3n+1+![]() ,
,
Tn=![]() ·3n+1+
·3n+1+![]() +
+![]() .
.


科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前n项和为
的前n项和为![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)令![]() 问是否存在正数m,使得
问是否存在正数m,使得![]() 对一切正整数n都成立?若存在,求出m的取值范围;若不存在,请说明理由.
对一切正整数n都成立?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
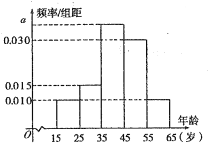
(1)求出![]() 的值;
的值;
(2)求这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求这2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点, ![]() 为椭圆
为椭圆![]() 的上顶点,点
的上顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() 为坐标原点,且
为坐标原点,且![]() ,
, ![]() .
.
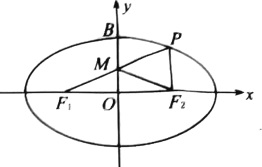
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线分别与椭圆
作两条互相垂直的直线分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点(异于点
两点(异于点![]() ),证明:直线
),证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f '(x)的图象如图所示,f(-1)=f(2)=3,令g(x)=(x-1)f(x),则不等式g(x)≥3x-3的解集是( )

A. [-1,1]∪[2,+∞)B. (-∞,-1]∪[1,2]
C. (-∞,-1]∪[2,+∞)D. [-1,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出2个小球,每个小球被取出的可能性相等.
(1)求从甲盒中取出的两个球上的编号不都是奇数的概率;
(2)求从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,若Sm-1=-4,Sm=0,Sm+2=14(m≥2,且m∈N*).
(1)求m的值;
(2)若数列{bn}满足![]() =log2bn(n∈N*),求数列{(an+6)·bn}的前n项和.
=log2bn(n∈N*),求数列{(an+6)·bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.若![]() 是函数
是函数![]() 的零点,则
的零点,则![]() 是
是![]() 的整数倍
的整数倍
B.函数![]() 的图象关于点
的图象关于点![]() 对称
对称
C.函数![]() 的图象与函数
的图象与函数![]() 的图象相同
的图象相同
D.函数![]() 的图象可由
的图象可由![]() 的图象先向上平移
的图象先向上平移![]() 个单位长度,再向左平移
个单位长度,再向左平移![]() 个单位长度得到
个单位长度得到
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com