
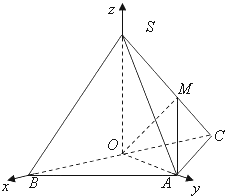
【题目】如图,在三棱锥S﹣ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. (Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求二面角A﹣SC﹣B的余弦值.
【答案】证明: (Ⅰ)由题设AB=AC=SB=SC=SA,连接OA,△ABC为等腰直角三角形,
所以 ![]() ,且AO⊥BC,
,且AO⊥BC,
又△SBC为等腰三角形,故SO⊥BC,
且 ![]() ,从而OA2+SO2=SA2 .
,从而OA2+SO2=SA2 .
所以△SOA为直角三角形,SO⊥AO.
又AO∩BO=O.
所以SO⊥平面ABC.
(Ⅱ)解:
以O为坐标原点,射线OB,OA分别为x轴、y轴的正半轴,
建立如图的空间直角坐标系O﹣xyz.
设B(1,0,0),则C(﹣1,0,0),A(0,1,0),S(0,0,1).SC的中点 ![]() ,
, ![]() .
.
∴ ![]() .
.
故 ![]() 等于二面角A﹣SC﹣B的平面角.
等于二面角A﹣SC﹣B的平面角.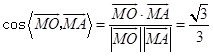 ,
,
所以二面角A﹣SC﹣B的余弦值为 ![]() .
.
【解析】(1)欲证SO⊥平面ABC,根据直线与平面垂直的判定定理可知只需证SO与平面ABC内两相交直线垂直,而SO⊥BC,SO⊥AO,又AO∩BO=O,满足定理条件;(2)以O为坐标原点,射线OB,OA分别为x轴、y轴的正半轴,建立空间直角坐标系O﹣xyz,求出两半平面的法向量,求出两法向量的夹角即可.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).


科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为( ) 
A.8+8 ![]() +4
+4 ![]()
B.8+8 ![]() +2
+2 ![]()
C.2+2 ![]() +
+ ![]()
D.![]() +
+ ![]() +
+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为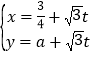 ,(
,(![]() 为参数),圆
为参数),圆![]() 的标准方程为
的标准方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与的交点为
与的交点为![]() ,与圆
,与圆![]() 的交点为
的交点为![]() ,且点
,且点![]() 恰好为线段
恰好为线段![]() 的中点,求
的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知⊙O:x2+y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且 ![]() . (Ⅰ)求点N的轨迹C的方程;
. (Ⅰ)求点N的轨迹C的方程;
(Ⅱ)若A(2,1),B(3,0),过B的直线与曲线C相交于D、E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄(单位:岁)分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)请根据频率分布直方图,估计这100名志愿者样本的平均数;
(3)在(1)的条件下,该市决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.(参考数据:![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且
且![]() .
.
![]() 当
当![]() 时,函数
时,函数![]() 恒有意义,求实数
恒有意义,求实数![]() 的取值范围;
的取值范围;
![]() 是否存在这样的实数
是否存在这样的实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上为减函数,并且最大值为1?如果存在,试求出
上为减函数,并且最大值为1?如果存在,试求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com