分析:(Ⅰ)将点代入到函数解析式中即可;
(Ⅱ)比较代数式大小时,可以用作差的方法.
解答:解:解法一:
(Ⅰ)由已知得a
n+1=a
n+1、即a
n+1-a
n=1,又a
1=1,
所以数列{a
n}是以1为首项,公差为1的等差数列.
故a
n=1+(n-1)×1=n.
(Ⅱ)由(Ⅰ)知:a
n=n从而b
n+1-b
n=2
n.
b
n=(b
n-b
n-1)+(b
n-1-b
n-2)+…+(b
2-b
1)+b
1=2
n-1+2
n-2+…+2+1
=
=2n-1∵b
n•b
n+2-b
n+12=(2
n-1)(2
n+2-1)-(2
n+1-1)
2=(2
2n+2-2
n-2
n+2+1)-(2
2n+2-2•2
n+1+1)
=-2
n<0
∴b
n•b
n+2<b
n+12解法二:
(Ⅰ)同解法一.
(Ⅱ)∵b
2=1
b
n•b
n+2-b
n+12=(b
n+1-2
n)(b
n+1+2
n+1)-b
n+12
=2n+1•bn+1-2n•bn+1-2n•2n+1=2
n(b
n+1-2
n+1)
=2
n(b
n+2
n-2
n+1)
=2
n(b
n-2
n)
=…
=2
n(b
1-2)
=-2
n<0
∴b
n•b
n+2<b
n+12 点评:高考考点:本小题主要考查等差数列、等比数列等基本知识,考查转化与化归思想,考查推理与运算能力.
易错提醒:第二问中的比较大小直接做商的话还要说明bn的正负,而往往很多学生不注意.
备考提示:对于递推数列要学生掌握常见求法,至少线性的要懂得处理.



 科学实验活动册系列答案
科学实验活动册系列答案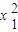 +
+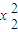 +…+
+…+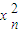 ,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B;
,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B;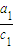 +
+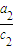 +
+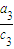 的最小值为3;
的最小值为3;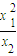 +
+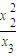 +…+
+…+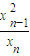 +
+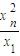 的最小值为
的最小值为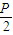 .
.