
【题目】如图1,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() ,如图2.
,如图2.
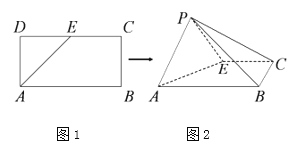
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+2)x+alnx(a∈R).
(1)若x=![]() 是函数f(x)的一个极值点,求实数a的值;
是函数f(x)的一个极值点,求实数a的值;
(2)当a>0时,讨论函数f(x)的单调性;
(3)当a>2且x>1时,求证:函数f(x)的最小值小于﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的实轴长为4,焦距为
的实轴长为4,焦距为![]() .
.
(1)求椭圆C的标准方程;
(2)设直线l经过点![]() 且与椭圆C交于不同的两点M,N(异于椭圆的左顶点),设点Q是x轴上的一个动点.直线QM,QN的斜率分别为
且与椭圆C交于不同的两点M,N(异于椭圆的左顶点),设点Q是x轴上的一个动点.直线QM,QN的斜率分别为![]() ,
,![]() ,试问:是否存在点Q,使得
,试问:是否存在点Q,使得![]() 为定值?若存在.求出点Q的坐标及定值;若不存在,请说明理由.
为定值?若存在.求出点Q的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本![]() 万元(不含促销费用),每件产品的销售价格定为
万元(不含促销费用),每件产品的销售价格定为![]() 元.
元.
(Ⅰ)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数(利润=总售价-成本-促销费);
万元的函数(利润=总售价-成本-促销费);
(Ⅱ)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛,图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
(1)完成下列![]() 的列联表,并回答是否有
的列联表,并回答是否有![]() 的把握认为“两个学段的学生对四大名著的了解有差异”?
的把握认为“两个学段的学生对四大名著的了解有差异”?
成绩小于60分的人数 | 成绩不小于60的人数 | 合计 | |
初中年级 | |||
高中年级 | |||
合计 |
(2)规定竞赛成绩不少于70分的为优秀,按分层抽样的方法从高中,初中年级优秀学生中抽取5人进行复赛,在复赛人员中选3人进行面试,记面试人员中来自初中段的为随机变量X,求随机变量X的分布列与期望.
![]() 其中
其中![]()
附表:
| 0.10 | 0.05 | span>0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(Ⅰ)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250支,还是255支百合花,四月后20天百合花销售总利润会更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() (a为正常数)与
(a为正常数)与![]() 在x轴上方仅有一个公共点P.
在x轴上方仅有一个公共点P.
(1)求实数m的取值范围(用a表示);
(2)O为原点,若![]() 与x轴的负半轴交于点A,当
与x轴的负半轴交于点A,当![]() 时,试求△OAP的面积的最大值(用a表示).
时,试求△OAP的面积的最大值(用a表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com