
【题目】对于函数f(x)=  ,有下列5个结论: ①任取x1 , x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;
,有下列5个结论: ①任取x1 , x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;
②函数y=f(x)在区间[4,5]上单调递增;
③f(x)=2kf(x+2k)(k∈N+),对一切x∈[0,+∞)恒成立;
④函数y=f(x)﹣ln(x﹣1)有3个零点;
⑤若关于x的方程f(x)=m(m<0)有且只有两个不同实根x1 , x2 , 则x1+x2=3.
则其中所有正确结论的序号是 . (请写出全部正确结论的序号)
【答案】①④⑤
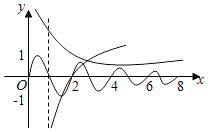
【解析】解:f(x)= 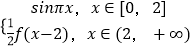 的图象如图所示:①∵f(x)的最大值为1,最小值为﹣1,
的图象如图所示:①∵f(x)的最大值为1,最小值为﹣1,
∴任取x1、x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2恒成立,故①正确;②函数在区间[4,5]上的单调性和[0,1]上的单调性相同,则函数y=f(x)在区间[4,5]上不单调;故②错误;③f( ![]() )=2f(
)=2f( ![]() +2)=4f(
+2)=4f( ![]() +4)=6f(
+4)=6f( ![]() +6)≠8f(
+6)≠8f( ![]() +8),故不正确;故③错误,④如图所示,函数y=f(x)﹣ln(x﹣1)有3个零点;故④正确,⑤当1≤x≤2时,函数f(x)关于x=
+8),故不正确;故③错误,④如图所示,函数y=f(x)﹣ln(x﹣1)有3个零点;故④正确,⑤当1≤x≤2时,函数f(x)关于x= ![]() 对称,若关于x的方程f(x)=m(m<0)有且只有两个不同实根x1,x2,
对称,若关于x的方程f(x)=m(m<0)有且只有两个不同实根x1,x2,
则 ![]() =
= ![]() ,则x1+x2=3成立,故⑤正确,
,则x1+x2=3成立,故⑤正确,
所以答案是:①④⑤.
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案,需要熟知两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x20的均值和方差分别为1和8,若yi=2xi+3(i=1,2,…,20),则y1 , y2 , …,y20的均值和方差分别是( )
A.5,32
B.5,19
C.1,32
D.4,35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 点(an , Sn)(n∈N*)都在函数f(x)= ![]() 的图象上.
的图象上.
(1)求数列{an}的通项公式;
(2)若bn=an3n , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为得到函数y=sin(2x﹣ ![]() )的图象,只需将函数y=sin2x的图象( )
)的图象,只需将函数y=sin2x的图象( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程x2+ax﹣ ![]() +1=0.
+1=0.
(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程中有实根的概率;
(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,f(x)=aln(x﹣1)+x,f′(2)=2
(1)求a的值,并求曲线y=f(x)在点(2,f(2))处的切线方程y=g(x);
(2)设h(x)=mf′(x)+g(x)+1,若对任意的x∈[2,4],h(x)>0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元. (Ⅰ)求y关于r的函数关系,并求其定义域;
(Ⅱ)求建造费用最小时的r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足对任意的n∈N* , 都有a13+a23++an3=(a1+a2++an)2且an>0.
(1)求a1 , a2的值;
(2)求数列{an}的通项公式;
(3)若bn= ![]() ,记Sn=
,记Sn= ![]() ,如果Sn<
,如果Sn< ![]() 对任意的n∈N*恒成立,求正整数m的最小值.
对任意的n∈N*恒成立,求正整数m的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com