
【题目】已知![]() (
(![]() 为常数).
为常数).
(1)求![]() 的极值;
的极值;
(2)设![]() ,记
,记![]() ,已知
,已知![]() 为函数
为函数![]() 是两个零点,求证:
是两个零点,求证: ![]() .
.
【答案】(1)![]() 的极大值为
的极大值为![]() ,无极小值;(2)见解析.
,无极小值;(2)见解析.
【解析】试题分析:(1) 求导,判断单调性得极值即可.
(2) 先在![]() 上构造函数
上构造函数![]() 和
和![]() 比较大小,再在
比较大小,再在![]() 上利用函数
上利用函数![]() 单调性得
单调性得![]() .
.
试题解析:(1)![]() ,由
,由![]() 得
得![]() ,
,
且![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() .
.
故函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
所以,函数![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(2)由![]() 及(1)知
及(1)知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
由条件知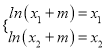 ,即
,即![]() ,
,
构造函数![]() ,知
,知![]() 与
与![]() 图像两交点的横坐标为
图像两交点的横坐标为![]() ,
, ![]() ,
,
![]() ,由
,由![]() 得
得![]() ,易知函数
,易知函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
欲证![]() ,只需证
,只需证![]() ,不妨设
,不妨设![]() ,
,
考虑到![]() 在
在![]() 上递增,只需证
上递增,只需证![]() ,
,
由![]() 知,只需证
知,只需证![]() ,
,
令![]() ,
,
则![]() ,
,
即![]() 单调增,注意到
单调增,注意到![]() ,
,
结合![]() 知
知![]() ,即
,即![]() 成立,
成立,
即![]() 成立.
成立.
点睛:本题考查的是函数的极值问题和极值点偏移问题.求极值时要注意判断在导数为![]() 的点两侧的符号,异号时为极值点,要记得判断是极大值还是极小值 ,否则不是极值点;在第二问极值点偏移中,要解决两个问题,一是在
的点两侧的符号,异号时为极值点,要记得判断是极大值还是极小值 ,否则不是极值点;在第二问极值点偏移中,要解决两个问题,一是在![]() 上构造函数
上构造函数![]() 和
和![]() 比较大小,二是在
比较大小,二是在![]() 上利用函数
上利用函数![]() 单调性.
单调性.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某校举行了以“重温时代经典,唱响回声嘹亮”为主题的“红歌”歌咏比赛. 该校高一年级有1,2,3,4四个班参加了比赛,其中有两个班获奖. 比赛结果揭晓之前,甲同学说:“两个获奖班级在2班、3班、4班中”,乙同学说:“2班没有获奖,3班获奖了”,丙同学说:“1班、4班中有且只有一个班获奖”,丁同学说:“乙说得对”. 已知这四人中有且只有两人的说法是正确的,则这两人是
A. 乙,丁 B. 甲,丙 C. 甲,丁 D. 乙,丙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为曲线
为曲线![]() 上任意一点,且
上任意一点,且![]() 到定点
到定点![]() 的距离比到
的距离比到![]() 轴的距离多1.
轴的距离多1.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 分别作倾斜角互补的直线
分别作倾斜角互补的直线![]() ,
, ![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
, ![]() 两点,过点
两点,过点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①频率是反映事件发生的频繁程度,概率反映事件发生的可能性大小;
②做n次随机试验,事件A发生m次,则事件A发生的频率![]() 就是事件A的概率;
就是事件A的概率;
③百分率是频率,但不是概率;
④频率是不能脱离n次试验的试验值,而概率是具有确定性的不依赖于试验次数的理论值;
⑤频率是概率的近似值,概率是频率的稳定值.
其中正确的是____(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 上顶点为
上顶点为![]() ,右顶点为
,右顶点为![]() ,离心率
,离心率![]() ,
, ![]() 为坐标原点,圆
为坐标原点,圆![]() :
: ![]() 与直线
与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 相交于
相交于![]() 两不同点,若椭圆
两不同点,若椭圆![]() 上一点
上一点![]() 满足
满足![]() ,求
,求![]() 面积的最大值及此时的
面积的最大值及此时的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com