
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)已知![]() 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当![]() 时,有
时,有![]() .若
.若![]() ,且
,且![]() ,求函数
,求函数![]()
![]() 的反函数;
的反函数;
(3)若在![]() 上存在
上存在![]() 个不同的点
个不同的点![]() ,
,![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)直接利用绝对值不等式的解法及应用求出结果.
(2)利用函数的周期和函数的关系式的应用求出函数的反函数.
(3)利用绝对值不等式的应用和函数的性质的应用,利用分类讨论思想的应用求出结果.
解:(1)解不等式![]()
当![]() 时,
时,![]() ,所以
,所以![]()
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
综上,该不等式的解集为![]()
(2)当![]() 时,
时,![]() ,
,
因为![]() 是以2为周期的偶函数,
是以2为周期的偶函数,
所以![]() ,
,
由![]() ,且
,且![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]()
所以当![]() 时,
时,
![]() ,
,
所以函数![]() 的反函数为
的反函数为
![]()
(3)①当![]() 时,在
时,在![]() 上
上![]() ,是
,是![]() 上的增函数,所以
上的增函数,所以
![]()
所以![]() ,得
,得![]() ;
;
②当![]() 时,在
时,在![]() 上
上![]() ,是
,是![]() 上的增函数,所以
上的增函数,所以
![]()
所以![]() ,得
,得![]() ;
;
③当![]() 时,
时,![]() 在
在![]() 上不单调,所以
上不单调,所以
![]()
![]() ,
,![]() ,
,
在![]() 上,
上,![]() .
.
![]() ,不满足.
,不满足.
综上,![]() 的取值范围为
的取值范围为![]() .
.
③当![]() 时,则
时,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,于是
上单调递减,于是![]()
![]()
令![]() ,解得
,解得![]() 或
或![]() ,不符合题意;
,不符合题意;
④当![]() 时,
时,![]() 分别在
分别在![]() 、
、![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]()
![]()
![]()
令![]() ,解得
,解得![]() 或
或![]() ,不符合题意.
,不符合题意.
综上,所求实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线l过点
的直线l过点![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程(
的参数方程(![]() 为常数)和曲线
为常数)和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求倾斜角
,求倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,长轴长为4,
,长轴长为4,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,点
的左,右焦点,点![]() 是椭圆
是椭圆![]() 上的任意一点,
上的任意一点,![]() 面积的最大为
面积的最大为![]() ,且取得最大值时
,且取得最大值时![]() 为钝角.
为钝角.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,过点
上任意一点,过点![]() 的切线分别交椭圆
的切线分别交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的平面展开图如图所示,其中四边形 ABCD 为正方形, E F 分别为PB PC 的中点,在此几何体中,下面结论中一定正确的是( )
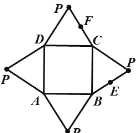
A.直线 AE 与直线 DF 平行B.直线 AE 与直线 DF 异面
C.直线 BF 和平面 PAD 相交D.直线 DF 平面 PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县应国家号召,积极开展了建设新农村活动,实行以奖代补,并组织有关部门围绕新农村建设中的三个方面(新设施,新环境,新风尚)对各个村进行综合评分,高分(大于88分)的村先给予5万元的基础奖励,然后比88分每高一分,奖励增加5千元,低分(小于等于75分)的村给予通报,取消5万元的基础奖励,且比75分每低1分,还要扣款1万元,并要求重新整改建设,分数在![]() 之间的只享受5万元的基础奖励,下面是甲、乙两个乡镇各10个村的得分数据(单位:分):
之间的只享受5万元的基础奖励,下面是甲、乙两个乡镇各10个村的得分数据(单位:分):
甲:62,74,86,68,97,75,88,98,76,99;
乙:71,81,72,86,91,77,85,78,83,84.
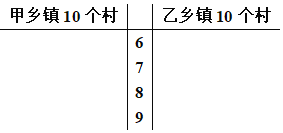
(1)根据上述数据完成如图的茎叶图,并通过茎叶图比较两个乡镇各10个村的得分的平均值及分散程度;(不要求计算具体的数值,只给出结论即可)
(2)为继续做好新农村的建设工作,某部门决定在这两个乡镇中任选两个低分村进行帮扶重建,求抽取的两个村中,两个乡镇中各有一个村的概率;
(3)从获取奖励的角度看,甲、乙两个乡镇哪个获取的奖励多?(需写出计算过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)求过点![]() 和函数
和函数![]() 的图像相切的直线方程;
的图像相切的直线方程;
(2)若对任意![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若存在唯一的整数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com