
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() ,
, ![]() ,过点
,过点![]() 作直线
作直线![]() ,
, ![]() 为直线
为直线![]() 上一动点.
上一动点.
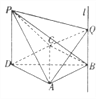
(1)求证: ![]() ;
;
(2)当二面角![]() 的大小为
的大小为![]() 时,求
时,求![]() 的长;
的长;
(3)在(2)的条件下,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:
(1)利用三垂线定理结合![]() 即可证得
即可证得![]() ;
;
(2)首先写出二面角的平面角,最后利用余弦定理列出方程求解QB的长度即可;
(3)将问题转化为两个三棱锥的体积,其中公共的底为△POQ,高的总长度为AC的长,则体积公式为: ![]()
试题解析:
(1)由题意知直线![]() 在面
在面![]() 上的射影为
上的射影为![]() ,
,
又菱形![]() 中
中![]() ,由三垂线定理知
,由三垂线定理知![]() .
.
(2)![]() 和
和![]() 都是以
都是以![]() 为底的等腰三角形,设
为底的等腰三角形,设![]() 和
和![]() 的交点为
的交点为![]() ,
,

连接![]() ,则
,则![]() 是二面角
是二面角![]() 的平面角,
的平面角,
由![]() 知,二面角
知,二面角![]() 大于
大于![]() ,
,
所以点![]() 与点
与点![]() 在平面
在平面![]() 的同侧,如图所示.
的同侧,如图所示.
则![]() 是二面角
是二面角![]() 的平面角,故
的平面角,故![]() .
.
在![]() 中,
中, ![]() ,设
,设![]() ,则
,则![]() 中,
中, ![]() ,
,
在直角梯形![]() 中,
中, ![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,故
,故![]() 且
且![]() ,
,
解得![]() ,即
,即![]() .
.
(3)由(2)知: ![]() ,
, ![]() ,
,
且![]() 面
面![]() ,∴
,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四凌锥S﹣ABCD中,底面ABCD是直角梯形,AD∥BC,SA⊥CD,AB⊥平面SAD,M是SC的中点,且SA=AB=BC=2,AD=1. 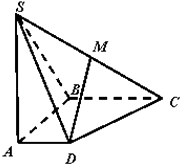
(1)求证:DM∥平面SAB;
(2)求四棱锥S﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中:
翻折过程中:

①![]() 是定值;②点
是定值;②点![]() 在某个球面上运动;
在某个球面上运动;
③存在某个位置,使![]() ;④存在某个位置,使
;④存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
, ![]() ,
, ![]() ,
, ![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”
作品获得一等奖”
乙说:“![]() 作品获得一等奖”
作品获得一等奖”
丙说:“![]() ,
, ![]() 两项作品未获得一等奖”
两项作品未获得一等奖”
丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子原件生产厂生产的10件产品中,有8件一级品,2件二级品,一级品和二级品在外观上没有区别.从这10件产品中任意抽检2件,计算:
(1)2件都是一级品的概率;
(2)至少有一件二级品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,an=32,sn=63,
(1)若数列{an}为公差为11的等差数列,求a1;
(2)若数列{an}为以a1=1为首项的等比数列,求数列{am2}的前m项和sm′ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
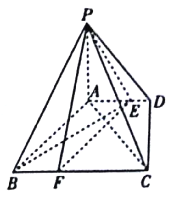
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com