定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy,f(xy)=f(x)f(y) (x,y∈R),且当x≠o时,f(x)≠0.
(1)求证:f(0)=0
(2)证明:f(x)是偶函数.并求f(x)的表达式
(3)若f(x)=alnx有两个不同实数解,求a的取值范围.
解:(1)∵f(x+y)=f(x)+f(y)+2xy,令x=y=0,
∴f(0)=2f(0)
∴f(0)=0;
(2)令x=y=1代入f(xy)=f(x)f(y)∴f(1)=f(1)
2,
∵当x≠0时,f(x)≠0,
∴f(1)=1,
令y=x代入f(x+y)=f(x)+f(y)+2xy,f(xy)=f(x)f(y) (x,y∈R),
f(2x)=2f(x)+2x
2,f(2x)=f(2)f(x),
∴f(2)f(x)=2f(x)+2x
2,
∵f(2)=2f(1)+2=4,
∴f(x)=x
2,f(-x)=f(x)
∴f(x)为偶函数;
(3)∵f(x)=alnx有两个不同实数解,
∴令h(x)=f(x)-alnx=x
2-xlnx,
∴h′(x)=2x-

,令h′(x)=0,
解得x=±
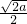
,
当-
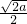
<x<
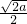
时,h′(x)<0,f(x)单调减函数;
当x≥
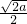
或x≤-
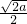
时,h′(x)>0,f(x)单调增函数;
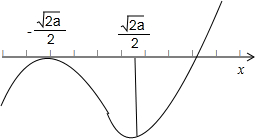
如下图:要求h(x)与x轴有两个交点,
可得h(-
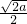
)=0,
∴a=
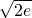
分析:(1)令x=y=0代入f(x+y)=f(x)+f(y)+2xy,即可求解;
(2)求出f(x)的表达式再判断奇偶性,由f(xy)=f(x)f(y),令x=y=1,得f(1)=1,再令y=x,代入f(x+y)=f(x)+f(y)+2xy,求出f(x),即可求解.
(3)令h(x)=f(x)-alnx,对其求导,求出h(x)的单调区间,画出草图,即可求解;
点评:此题考查抽象函数的问题,这类题一般都利用特殊值法,先求出几个特殊值f(0),f(1)等,看似很难其实比较简单,最后一问用到了利用导数来求函数的单调区间,其中构造函数h(x)很关键.

 解:(1)∵f(x+y)=f(x)+f(y)+2xy,令x=y=0,
解:(1)∵f(x+y)=f(x)+f(y)+2xy,令x=y=0, ,令h′(x)=0,
,令h′(x)=0,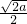 ,
,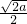 <x<
<x<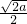 时,h′(x)<0,f(x)单调减函数;
时,h′(x)<0,f(x)单调减函数;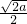 或x≤-
或x≤-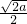 时,h′(x)>0,f(x)单调增函数;
时,h′(x)>0,f(x)单调增函数;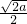 )=0,
)=0,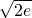


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案