
【题目】(本小题满分12分)某工厂某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(Ⅰ)写出年利润
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(Ⅰ)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
【答案】(1)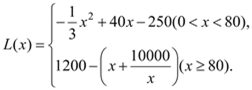 ;(2)100.
;(2)100.
【解析】试题分析:(Ⅰ)分两种情况进行研究,当0<x<80时,投入成本为C(x)=![]() (万元),根据年利润=销售收入﹣成本,列出函数关系式,当x≥80时,投入成本为C(x)=51x+
(万元),根据年利润=销售收入﹣成本,列出函数关系式,当x≥80时,投入成本为C(x)=51x+![]() ,根据年利润=销售收入﹣成本,列出函数关系式,最后写成分段函数的形式,从而得到答案;
,根据年利润=销售收入﹣成本,列出函数关系式,最后写成分段函数的形式,从而得到答案;
(Ⅱ)根据年利润的解析式,分段研究函数的最值,当0<x<80时,利用二次函数求最值,当x≥80时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
解:(Ⅰ)∵每件商品售价为0.05万元,
∴x千件商品销售额为0.05×1000x万元,
①当0<x<80时,根据年利润=销售收入﹣成本,
∴L(x)=(0.05×1000x)﹣![]() ﹣10x﹣250=
﹣10x﹣250=![]() +40x﹣250;
+40x﹣250;
②当x≥80时,根据年利润=销售收入﹣成本,
∴L(x)=(0.05×1000x)﹣51x﹣![]() +1450﹣250=1200﹣(x+
+1450﹣250=1200﹣(x+![]() ).
).
综合①②可得,L(x)=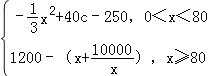 .
.
(Ⅱ)由(Ⅰ)可知,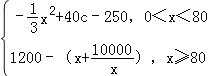 ,
,
①当0<x<80时,L(x)=![]() +40x﹣250=﹣
+40x﹣250=﹣![]() ,
,
∴当x=60时,L(x)取得最大值L(60)=950万元;
②当x≥80时,L(x)=1200﹣(x+![]() )≤1200﹣2
)≤1200﹣2![]() =1200﹣200=1000,
=1200﹣200=1000,
当且仅当x=![]() ,即x=100时,L(x)取得最大值L(100)=1000万元.
,即x=100时,L(x)取得最大值L(100)=1000万元.
综合①②,由于950<1000,
∴当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)满足:
①对任意实数m,n都有f(m+n)+f(m﹣n)=2f(m)f(n);
②对任意m∈R,都有f(1+m)=f(1﹣m)恒成立;
③f(x)不恒为0,且当0<x<1时,f(x)<1.
(1)求f(0),f(1)的值;
(2)判断函数f(x)的奇偶性,并给出你的证明;
(3)定义:“若存在非零常数T,使得对函数g(x)定义域中的任意一个x,均有g(x+T)=g(x),则称g(x)为以T为周期的周期函数”.试证明:函数f(x)为周期函数,并求出 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A′,连接EF,A′B. 
(1)求证:A′D⊥EF;
(2)求二面角A′﹣EF﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在冬季供暖时减少能量损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位:![]() )满足关系:
)满足关系:![]() ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:①y= ![]() 是奇函数;
是奇函数;
②若α,β是第一象限角,且α>β,则cosα<cosβ;
③函数f(x)=2x﹣x2在R上有3个零点;
④函数y=sin2x的图象向左平移 ![]() 个单位,得到函数
个单位,得到函数 ![]() 的图象.
的图象.
其中正确命题的序号是 . (把正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段内,某公路汽车的车流量y(千辆/h)与汽车的平均速度v(km/h)之间的函数关系式为 ![]() . (I)若要求在该段时间内车流量超过2千辆/h,则汽车在平均速度应在什么范围内?
. (I)若要求在该段时间内车流量超过2千辆/h,则汽车在平均速度应在什么范围内?
(II)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com