
 如图,倾斜角为α的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
如图,倾斜角为α的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.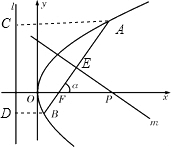
| 4 |
| 1-cosα |
| 4 |
| 1+cosα |
| |FA|+|FB| |
| 2 |
| 1 |
| 2 |
| 4cosα |
| sin2α |
| |FE| |
| cosα |
| 4 |
| sin2α |
| 4 |
| sin2α |


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
 如图,倾斜角为α的直线经过抛物线y2=4x的焦点,且与抛物线交于A、B两点,Q为A、B中点,
如图,倾斜角为α的直线经过抛物线y2=4x的焦点,且与抛物线交于A、B两点,Q为A、B中点,| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于点A(-1,0),点B(0,-1),PA与y轴交于点N,PB与x轴交于点M,设
(2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于点A(-1,0),点B(0,-1),PA与y轴交于点N,PB与x轴交于点M,设| PO |
| PM |
| PN |
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年重庆卷文)(12分)
如图,倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() 的焦点F,且与抛物线交于A、B两点。
的焦点F,且与抛物线交于A、B两点。

题(21)图
(Ⅰ)求抛物线的焦点F的坐标及准线l的方程;
(Ⅱ)若![]() 为锐角,作线段AB的垂直平分线m交x轴于点P,
为锐角,作线段AB的垂直平分线m交x轴于点P,
证明|FP||FP|cos2![]() 为定值,并求此定值。
为定值,并求此定值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市高三模拟考试(三模)理科数学试卷(解析版) 题型:解答题
如图,倾斜角为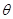 的直线
的直线 与单位圆在第一象限的部分交于点
与单位圆在第一象限的部分交于点 ,单位圆与坐标轴交于点
,单位圆与坐标轴交于点 ,点
,点 ,
, 与
与 轴交于点
轴交于点 ,
, 与
与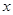 轴交于点
轴交于点 ,设
,设


(1)用角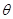 表示点
表示点 、点
、点 的坐标;
的坐标;
(2)求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com