
在 中,角
中,角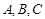 所对的边分别为
所对的边分别为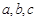 ,若
,若 。
。
(1)求证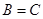 ;
;
(2)若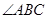 的平分线交
的平分线交 于
于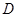 ,且
,且 ,求
,求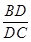 的值。
的值。
(1)利用正弦定理证明即可;(2) .
.
解析试题分析:(1)∵acosB+bcosA=b,由正弦定理可得 sinAcosB+cosAsinB=sinB,
∴sin(A+B)=sinB, 3分
即sinC=sinB,∴b=c,∴C=B. 6分
(2)△BCD中,用正弦定理可得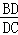 =
=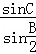 ,由第一问知道C=B,
,由第一问知道C=B,
而BD是角平分线,∴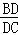 ="2cos"
="2cos" 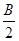 . 8分
. 8分
由于三角形内角和为180°,设 A=x,B=2α=C,那么4α+x=180°,
故α+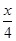 =45°.--9分
=45°.--9分
∵ ,∴
,∴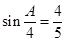 ,
,
∴cosα=cos(45°﹣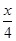 )=cos45°cos
)=cos45°cos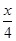 +sin45°sin
+sin45°sin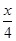 =
=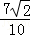 .
.
∴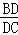 =2cos
=2cos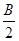 =2cosα=
=2cosα= . 12分
. 12分
考点:本题考查了正余弦定理的综合运用
点评:此类问题比较综合,不仅考查了学生对三角函数的变换,还考查了正余弦定理的运用,考查了学生的综合分析能力及解题能力


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com