
����Ŀ��Ϊ�˽������ͯ�ķ����Ƿ��볣��̼�������йأ��ֶ�100�����꼶ѧ���������ʾ�����õ���ͼ��������ƽ��ÿ���500ml����Ϊ���ȣ����س���50kgΪ���֣���֪��ȫ��100���������ȡ1�ˣ��鵽���ֵ�ѧ���ĸ���Ϊ0.8��
���� | ������ | �ϼ� | |
���� | 60 | ||
������ | 10 | ||
�ϼ� | 100 |
��1�������ѧ���������������������������������
��2���Ƿ���95%�İ�����Ϊ�����볣��̼�������йأ�˵��������ɣ� �����ο���ʽ��x2= ![]()
P��x2��x0�� | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡�
��1���⣺��ȫ��100���������ȡ1�ˣ��鵽���ֵ�ѧ���ĸ���Ϊ0.8������ֵ�ѧ��Ϊ80�ˣ�
���� | ������ | �ϼ� | |
���� | 60 | 20 | 80 |
���� | 10 | 10 | 20 |
�ϼ� | 70 | 30 | 100 |
��2���⣺����֪���ݿ���ã�K2= ![]() ��4.76��3.841��
��4.76��3.841��
�����95%�İ�����Ϊ�����볣��̼�������й�
����������1��������ȫ��100���������ȡ1�ˣ��鵽���ֵ�ѧ���ĸ���Ϊ0.8���������ֵ�ѧ�����������������������֣���2���������������������ݣ�������۲�ֵ�Ĺ�ʽ���ѹ۲�ֵͬ�ٽ�ֵ���бȽϣ��õ���95%�İ���˵��Ӫ��˵�����Ա��йأ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() �У�
�У� ![]() ƽ��
ƽ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��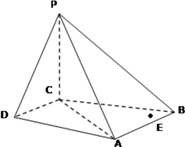
��1����֤�� ![]() ƽ��
ƽ�� ![]()
��2����֤��ƽ�� ![]() ƽ��
ƽ�� ![]()
��3����� ![]() Ϊ
Ϊ ![]() �е㣬����
�е㣬���� ![]() ���Ƿ���ڵ�
���Ƿ���ڵ� ![]() ��ʹ��
��ʹ�� ![]() ��ƽ��
��ƽ�� ![]() ��˵������.
��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=x3��ax+1�����䣨1��+�ޣ���������������ʵ��a��ȡֵ��Χ�ǣ� ��
A.a��3
B.a��3
C.a��3
D.a��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�۸������Ʒ��������֮��ļ���������������
�۸�x��Ԫ/kg�� | 10 | 15 | 20 | 25 | 30 |
��������y��kg�� | 11 | 10 | 8 | 6 | 5 |
��1����y����x�����Իع鷽�̣�
��2�����ã�1���еĻع鷽�̣����۸�x=40Ԫ/kgʱ����������y��Ԥ��ֵΪ���٣�
�ο���ʽ�����Իع鷽�� ![]() ������
������ 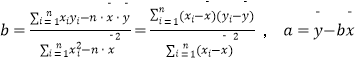 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�㣨x0 �� y0����x2+y2=r2��r��0���⣬��ֱ��x0x+y0y=r2��Բx2+y2=r2��λ�ù�ϵΪ�� ��
A.�ཻ
B.����
C.����
D.�ཻ�����С���������������п���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}������a1=1��ǰn���ΪSn �� �����㣨n+1��an=2Sn��n��N*����
��1��������{an}��ͨ�ʽ��
��2����bn=ancos����an����������{bn����ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��A1B1C1D1�У�����ABCDΪ�����Σ�DD1��ƽ��ABCD��AB=4��AA1=2����E1����C1D1�ϣ���D1E1=3��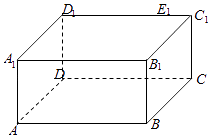
��������CD��ȷ��һ��E��ʹ��ֱ��EE1��ƽ��D1DB����д��֤�����̣�
����������F��������ABCD�ڣ���AF=2����˵����F�Ĺ켣��̽��E1F���ȵ���Сֵ�����ʱֱ��E1F��ƽ��ABCD���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��p��x��y����ֱ��kx+y+4=0��k��0����һ���㣬PA��PB��ԲC��x2+y2��2y=0���������ߣ�A��B���е㣬���ı���PACB����С�����2����k��ֵΪ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com