【题目】空气质量指数
是反映空气质量状况的指数，指数值越小，表明空气质量越好，其对应关系如表：
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市10月1日—20日指数变化趋势：
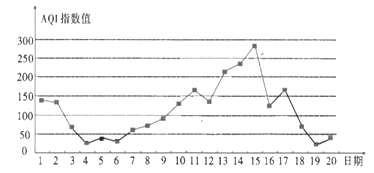
下列叙述正确的是（ ）
A.该市10月的前半个月的空气质量越来越好
B.这20天中的中度污染及以上的天数占
C.这20天中指数值的中位数略高于100
D.总体来说，该市10月上旬的空气质量比中旬的空气质量差
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】某公司为了了解年研发资金投人量
（单位：亿元）对年销售额
（单位：亿元）的影响.对公司近
年的年研发资金投入量
和年销售额
的数据，进行了对比分析，建立了两个函数模型：①
，②
，其中
、
、
、
均为常数，
为自然对数的底数.并得到一些统计量的值.令
，
，经计算得如下数据：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）请从相关系数的角度，分析哪一个模型拟合程度更好？
（2）（ⅰ）根据（1）的选择及表中数据，建立关于的回归方程；
（ⅱ）若下一年销售额需达到
亿元，预测下一年的研发资金投入量
是多少亿元？
附：①相关系数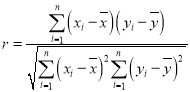
，
回归直线
中公式分别为：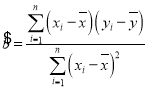
，
；
②参考数据：
，
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
,
满足
（
…）．
（1）若
，求
的值；
（2）若
且
，则数列
中第几项最小？请说明理由；
（3）若
（n=1,2,3,…），求证：“数列为等差数列”的充分必要条件是“数列
为等差数列且
（n=1,2,3,…）”．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于定义域为
的函数
，如果存在区间
，其中
，同时满足：
①
在
内是单调函数：②当定义域为时，的值域为，则称函数是区间上的“保值函数”，区间称为“保值函数”.
（1）求证：函数
不是定义域
上的“保值函数”；
（2）若函数
（
）是区间上的“保值函数”，求
的取值范围；
（3）对（2）中函数，若不等式
对
恒成立，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于函数
，若存在区间
，使得
，则称函数为“可等域函数”，区间
为函数的一个“可等域区间”．给出下列4个函数：
①
；②
； ③
； ④
．
其中存在唯一“可等域区间”的“可等域函数”为（ ）
（A）①②③ （B）②③ （C）①③ （D）②③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2018届安徽省合肥市高三第一次教学质量检测】一家大型购物商场委托某机构调查该商场的顾客使用移动支付的情况.调查人员从年龄在
内的顾客中，随机抽取了180人，调查结果如表：
（1）为推广移动支付，商场准备对使用移动支付的顾客赠送1个环保购物袋.若某日该商场预计有12000人购物，试根据上述数据估计，该商场当天应准备多少个环保购物袋？
（2）某机构从被调查的使用移动支付的顾客中，按分层抽样的方式抽取7人作跟踪调查，并给其中2人赠送额外礼品，求获得额外礼品的2人年龄都在
内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，且AB＝1，BC＝2， ∠ABC=60°，PA⊥平面ABCD，AE⊥PC于E，
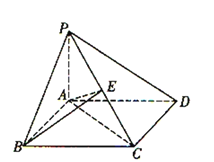
下列四个结论：①AB⊥AC；②AB⊥平面PAC；③PC⊥平面ABE；④BE⊥PC．正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，曲线C的参数方程为
（
为参数）．以坐标原点O为极，z轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
.
(Ⅰ)求曲线C的普通方程和直线的直角坐标方程；
(Ⅱ)设点
．若直线与曲线C相交于A，B两点，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的两个焦点为
,
,焦距为
,直线
:
与椭圆相交于
,
两点,
为弦
的中点.
（1）求椭圆的标准方程;
（2）若直线:
与椭圆相交于不同的两点
,
,
,若
（
为坐标原点）,求
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
