
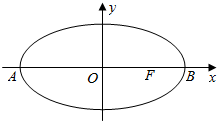
 在平面直角坐标系xOy中,如图,已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
在平面直角坐标系xOy中,如图,已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.分析 (1)设点P(x,y),由两点距离公式将PF2-PB2=4,变成坐标表示式,整理即得点P的轨迹方程;
(2)将${x_1}=2,{x_2}=\frac{1}{3}$分别代入椭圆方程,解出点M与点N的坐标,由两点式写出直线AM与直线BN的方程,联立解出交点T的坐标.
解答  解:(1)设点P(x,y),则F(2,0)、B(3,0)、A(-3,0).
解:(1)设点P(x,y),则F(2,0)、B(3,0)、A(-3,0).
由PF2-PB2=4,得(x-2)2+y2-[(x-3)2+y2]=4,
化简得x=$\frac{9}{2}$.
故所求点P的轨迹为直线x=$\frac{9}{2}$;
(2)将${x_1}=2,{x_2}=\frac{1}{3}$分别代入椭圆方程,以及y1>0,y2<0,
得M(2,$\frac{5}{3}$)、N($\frac{1}{3}$,-$\frac{20}{9}$),
直线MTA方程为:$\frac{y-0}{\frac{5}{3}-0}=\frac{x+3}{2+3}$,即y=$\frac{1}{3}$x+1,
直线NTB方程为:$\frac{y-0}{-\frac{20}{9}-0}=\frac{x-3}{\frac{1}{3}-3}$,即y=$\frac{5}{6}$x-$\frac{5}{2}$.
联立$\left\{\begin{array}{l}{y=\frac{1}{3}x+1}\\{y=\frac{5}{6}x-\frac{5}{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=7}\\{y=\frac{10}{3}}\end{array}\right.$,
点T的坐标为(7,$\frac{10}{3}$).
点评 本题考查椭圆的简单性质,考查直线与椭圆的方程等基础知识.考查运算求解能力和探究问题的能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com