
 x-y+
x-y+ =0或
=0或 x+y+
x+y+ =0
=0 ,求出∠ECF为直角,又CE=CF,可得出三角形ECF为等腰直角三角形,由CE及CF的长,利用勾股定理求出EF的长,再利用垂径定理得到D为EF中点,利用斜边上的中线等于斜边的一半求出CD的长,即为圆心距,设直线l的斜率为k,由A的坐标及k表示出直线l的方程,利用点到直线的距离公式表示出圆心C到直线l的距离d,让d等于CD的长列出关于k的方程,求出方程的解得到k的值,进而确定出直线l的方程.
,求出∠ECF为直角,又CE=CF,可得出三角形ECF为等腰直角三角形,由CE及CF的长,利用勾股定理求出EF的长,再利用垂径定理得到D为EF中点,利用斜边上的中线等于斜边的一半求出CD的长,即为圆心距,设直线l的斜率为k,由A的坐标及k表示出直线l的方程,利用点到直线的距离公式表示出圆心C到直线l的距离d,让d等于CD的长列出关于k的方程,求出方程的解得到k的值,进而确定出直线l的方程.
 ,
, ×360°=90°,又EC=FC=
×360°=90°,又EC=FC= ,
,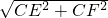 =2,
=2, EF=1,
EF=1,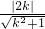 =1,即k2=
=1,即k2= ,
, ,
, x-y+
x-y+ =0或
=0或 x+y+
x+y+ =0.
=0. x-y+
x-y+ =0或
=0或 x+y+
x+y+ =0
=0

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
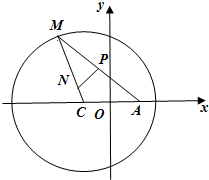 已知圆C:(x+1)2+y2=8.
已知圆C:(x+1)2+y2=8.| AM |
| AP |
| NP |
| AM |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com