Question

【题目】已知圆．

(1)若直线过点且被圆截得的弦长为2，求直线的方程；

(2)从圆外一点向圆引一条切线，切点为为坐标原点，满足，求点的轨迹方程及的最小值．

Answer 1

【答案】（1）x＝－2或3x－4y＋6＝0（2）2x－4y＋3＝0，

【解析】

（1）⊙C：x2+y2+2x﹣4y+3=0，化为标准方程，求出圆心C，半径r．分类讨论，利用C到l的距离为1，即可求直线l的方程；

（2）设P（x，y）．由切线的性质可得：CM⊥PM，利用|PM|=|PO|，可得3x+4y﹣12=0，求|PM|的最小值，即求|PO|的最小值，即求原点O到直线2x﹣4y+3=0的距离．

解：(1) (1)x2＋y2＋2x－4y＋3＝0可化为(x＋1)2＋(y－2)2＝2，

当直线l的斜率不存在时，其方程为x＝－2，

易求直线l与圆C的交点为A(－2，1)，B(－2，3)，|AB|＝2，符合题意；

当直线l的斜率存在时，设其方程为y＝k(x＋2)，即kx－y＋2k＝0，

则圆心C到直线l的距离，

解得，

所以直线l的方程为3x－4y＋6＝0

综上，直线l的方程为x＝－2或3x－4y＋6＝0

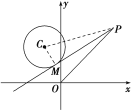
(2) 如图，PM为圆C的切线，连接MC，PC，则CM⊥PM，

所以△PMC为直角三角形，

所以|PM|2＝|PC|2－|MC|2

设P(x，y)，由(1)知C(－1，2)，|MC|＝，

因为|PM|＝|PO|，所以(x＋1)2＋(y－2)2－2＝x2＋y2，

化简得点P的轨迹方程为2x－4y＋3＝0

求|PM|的最小值，即求|PO|的最小值，也即求原点O到直线2x－4y＋3＝0的距离，

代入点到直线的距离公式可求得|PM|的最小值为.