
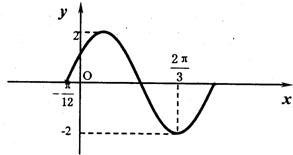
 如图,给出函数
如图,给出函数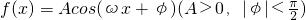 图象的一部分,则f(x)的解析式为f(x)=________.
图象的一部分,则f(x)的解析式为f(x)=________.
 T=
T= π求得周期,再由图象过点
π求得周期,再由图象过点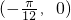 ,代入函数解析式求出φ.
,代入函数解析式求出φ. T=
T= π,故T=π,由公式可得ω=
π,故T=π,由公式可得ω= =2,故函数解析式为f(x)=2cos(2x+φ)
=2,故函数解析式为f(x)=2cos(2x+φ)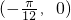 ,得f(
,得f(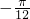 )=2cos(2×
)=2cos(2×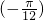 +φ)=0,即cos(
+φ)=0,即cos( +φ)=0
+φ)=0 +φ=-
+φ=- ,解得φ=
,解得φ= ,符合
,符合
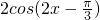
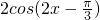 .
.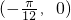 是增区间上的零点,故此点对应的相位是-
是增区间上的零点,故此点对应的相位是- .
. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图是某池塘中野生水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:
如图是某池塘中野生水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 给出下列5个命题:
给出下列5个命题:| 1 |
| 5 |
| 1 |
| 1-a |
| 2a |
tan2x+
| ||
|
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com